Задача 3. Построить линию пересечения пирамиды с прямой призмой

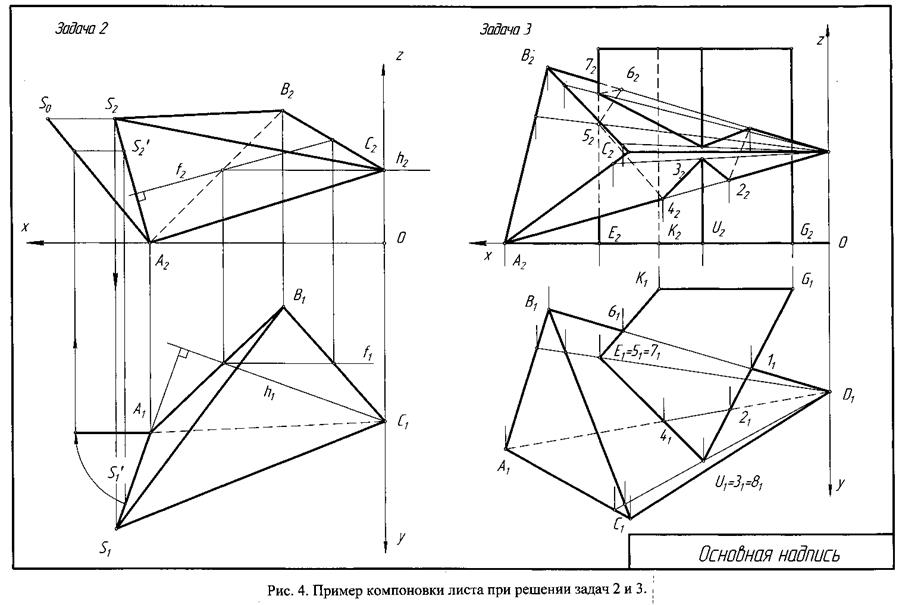
Построить линию пересечения пирамиды с прямой призмой. Данные для своего варианта взять из таблицы 3. Пример выполнения задачи при­веден на рис. 4.

Указания к решению задачи 3. В оставшейся правой половине лис­та намечаются оси координат и из таблицы 3 согласно своему варианту берутся координаты точек А, В, С и D вершин пирамиды и координаты то­чек E, K, G и U вершин многоугольника нижнего основания призмы. высота призмы равна 85 мм. По этим данным строятся проекции многогранников (пирамида и призма). Призма своим основанием стоит на плоскости

Таблица 3. Данные к задаче 3.

уровня, горизонтальные проекции ее вертикальных ребер преобразуется в точки. Грани боковой поверхности призмы представляют собой отсеки го­ризонтально проецирующих плоскостей.

Линия взаимного пересечения многогранников представляет собой пространственную замкнутую ломаную линию. Для ее построения сначала находят ее вершины, а затем в определенном порядке соединяют их отрез­ками прямых. Вершины этой линии могут быть определены как точки пе­ресечения ребер одного многогранника (пирамиды) с гранями другого (призмы). Соединяя каждые пары таких точек одних и тех же граней от­резками прямых, получаем линию пересечения многогранников.

Видимыми являются только те стороны многоугольника пересече­ния, которые принадлежат видимым граням многогранников. Их следует показать сплошными основными линиями красной пастой. Все вспомога­тельные построения на эпюре сохранить и показать их тонкими линиями.

ПРИМЕЧАНИЕ. Задаче 3 уделить особое внимание. Все построе­ния на чертеже тщательно проверить. Допущенные ошибки приводят к не­правильному решению следующих задач 4, 5 - «построение развертки многогранников».