
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача 9. Построить развертку конуса вращения
|
|
Построить развертку конуса вращения. Показать на развертке линии пересечения с цилиндром. В качестве исходных данных использовать результаты решения задачи 7.
Указания к решению задачи 9. На листе бумаги ватмана формата A3 строят развёртку поверхности. При решении данной задачи следует пользоваться методом триангуляции (метод построения приближенных разверток развертываемых поверхностей). Он состоит в том, что поверхность аппроксимируется многогранной поверхностью, состоящей из жестких неизменяемых граней.
Развертка конуса вращения.
В общем случае, разверткой поверхности конуса вращения является круговой сектор с углом 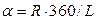 , где R - радиус окружности основания конуса вращения; L - длина образующей.
, где R - радиус окружности основания конуса вращения; L - длина образующей.
В данном случае, развертка конической поверхности должна быть выполнена как развертка вписанной в нее пирамиды (не менее чем 12-тигранной). При необходимости предварительно определяют истинные размеры ребер (образующих) способом вращения или методом прямоугольного треугольника.
На развертке конуса вращения строят прямолинейные образующие или параллели, проходящие через характерные точки линий пересечения конуса вращения с цилиндром вращения. Через такие точки проходят линии пересечения поверхностей в преобразовании (на развертке). Контур боковых поверхностей цилиндра и конуса вращения, а также их основания (окружности) обвести основной сплошной линией; линии пересечения заданных поверхностей обвести красной пастой, а все вспомогательные построения выполнить основными тонкими линиями. Пример решения задачи приведен на рис.12.
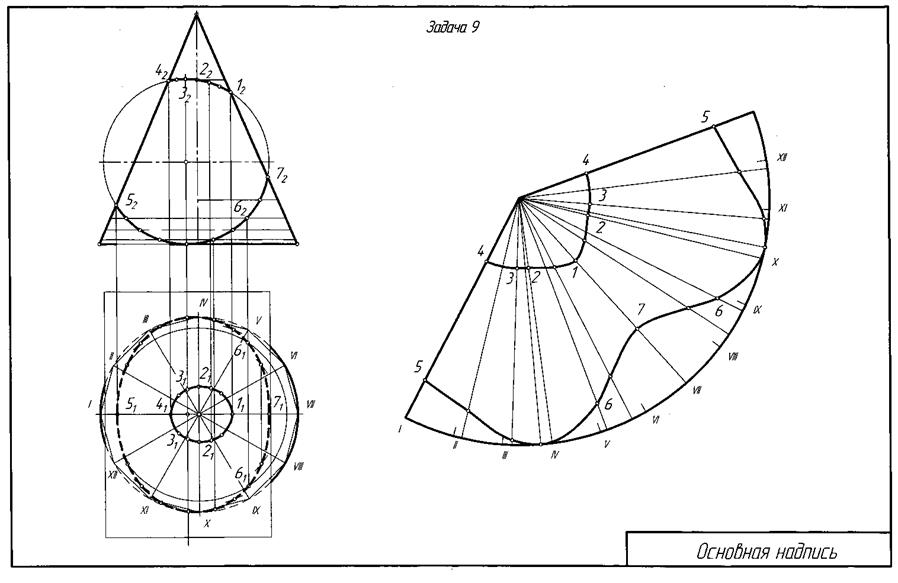
Рис.12. Пример решения задачи 9.
Вопросы для самопроверки
К теме 1. Введение. Центральные и параллельные проекции
1. Какие изображения называют рисунками, какие - чертежами?
2. Какие известны вам основные методы проецирования геометрических форм на плоскости?
3. Сформулируйте основные свойства параллельного проецирования.
4. Что называют обратимостью чертежа?
5. Сформулируйте и покажите на чертежах особенности методов ортогональных и аксонометрических проекций.
6. Что называют координатами точки пространства в декартовой системе координат?
7. Укажите основные свойства чертежей геометрических образов.
К теме 2. Точка. Прямая. Плоскость на эпюре Монжа
1. Постройте трехкартинный эпюр точек, расположенных в различных углах пространства; точек, расположенных в различных октантах.
2. Постройте чертежи отрезков прямых линий, расположенных в различных углах пространства.
3. Укажите частные положения отрезков прямых линий.
4. Какие прямые называют линиями уровня? Проецирующими прямыми?
5. Как изображаются на чертеже пересекающиеся, параллельные и
скрещивающиеся прямые линии?
6. Могут ли скрещивающиеся прямые линии иметь параллельные проекции на плоскостях П1 и П2?
7. Покажите способы задания плоскости общего положения и проецирующих плоскостей.
8. Как строят прямые линии и точки в плоскости?
9. Изложите особенности проецирующих плоскостей.
10. Покажите способы построения горизонтали, фронтали и линии наибольшего наклона плоскостей общего положения и проецирующих плоскостей.
К теме 3. Позиционные и метрические задачи
1. Покажите на примерах, как определяют точки пересечения проецирующих плоскостей прямыми линиями, линии пересечения проецирующих плоскостей плоскостями общего положения и проецирующими плоскостями.
2. Изобразите схему и укажите последовательность решения задачи на построение точки пересечения прямой с плоскостью общего положения.
3. Как определяют видимость элементов геометрических образов относительно плоскостей проекций?
4. Изобразите схему и укажите последовательность построения линии пересечения двух плоскостей.
5. Изобразите схему и приведите примеры построений прямых линий, параллельных и перпендикулярных плоскостям.
6. Сформулируйте условие параллельности и условие перпендикулярности двух плоскостей.
7. Сформулируйте условие перпендикулярности двух прямых общего положения.
8. Как определяются на чертеже расстояния от точки до проецирующей плоскости, плоскости общего положения?
9. Как определяются на чертеже расстояния от точки до прямой частного, общего положения?
К теме 4. Способы преобразования эпюра Монжа
1. В чем состоит принцип преобразования чертежа способом замены плоскостей проекций?
2. Что определяет направление новой плоскости проекций при переводе плоскости общего положения в проецирующие плоскости?
3. Какова схема решения задачи по определению углов наклона плоскости к плоскостям проекций способом замены плоскостей проекций?
4. Какова схема решения задачи по определению натуральной величины отсека произвольно расположенной плоскости способом замены плоскостей проекций?
5. В чем состоит принцип преобразования чертежа способом вращения вокруг проецирующих прямых?
6. Какую прямую принимают за ось вращения при переводе отсека плоскости из общего положения во фронтально проецирующую плоскость, в горизонтально проецирующую плоскость?
7. Можно ли считать плоскопараллельное перемещение вращением вокруг не выявленных осей (проецирующих прямых) и почему?
8. Укажите последовательность приемов определения натуральной величины отсека плоскости способом плоскопараллельного перемещения.
9. Какова последовательность приемов определения натуральной величины отсека плоскости способом вращения вокруг прямых, параллельных плоскости проекций?
К теме 5. Многогранники
1. Какие многогранники называют выпуклыми и выпукло вогнутыми?
2. Какие многогранники называют правильными?
3. Назовите правильные выпуклые многогранники.
4. Изложите сущность способов построения линии пересечения многогранников.
5. Что называют разверткой многогранной поверхности?
К теме 6. Кривые линии
1. Какие кривые линии называют алгебраическими?
2. Что называют порядком алгебраической кривой?
3. Что называют кривизной плоской кривой, и как ее определяют графически?
4. Приведите определение эволюты и эвольвенты плоской кривой, назовите основные свойства эволют и эвольвент.
5. Какие кривые называют овалами? Покажите примеры овалов.
6. Какие кривые называют кривыми второго порядка? Расскажите о каждой из них.
7. Какие кривые называют эквидистантными?
8. Как определяют на чертеже направление (ход) цилиндрической винтовой линии?
9. Расскажите о кривых линиях на сфере.
К теме 7. Поверхности. Образование и задание поверхностей
1. Каковы основные способы задания поверхностей?
2. Что называют каркасом поверхности?
3. Что называют определителем поверхности?
4. Назовите основные виды перемещений производящей линии.
5. Как образуются и задаются на чертеже поверхности переноса прямолинейного направления, поверхности вращения, винтовые поверхности?
6. Какие поверхности вращения называют поверхностями второго порядка?
7. Укажите основные свойства поверхностей вращения.
8. Какие поверхности называют тором?
9. Какие косые поверхности называют линейчатыми поверхностями с направляющей плоскостью? Какова схема построения положений производящей линии таких поверхностей?
10. Приведите определение поверхности второго порядка общего вида.
К теме 8. Пересечение поверхностей плоскостью и прямой
1. Укажите общую схему определения точек линии пересечения поверхности плоскостью.
2. Какие точки линии пересечения поверхности плоскостью называют главными (опорными)?
3. Укажите последовательность графических построений при определении точек пересечения прямой с поверхностью.
4. Укажите условия, при которых в сечении конуса вращения плоскостью получаются окружность, эллипс, гипербола, парабола, пересекающиеся прямые.
5. Укажите последовательность графических построений при определении линии пересечения плоскостями поверхностей второго порядка общего вида.
К теме 9. Взаимное пересечение поверхностей
1. Изобразите общую схему построения линий пересечения поверхностей.
2. Назовите основные способы построения линий пересечения поверхностей.
3. Опишите способы секущих плоскостей и сферических посредников при определении линии пересечения поверхностей.
4. Какое пересечение поверхностей называют полным и неполным?
5. Отметьте преимущество решения задач на построение линии пересечения поверхностей проецирующими цилиндрами и проецирующими призмами.
6. Покажите схемы построения линий пересечения двух конических поверхностей, имеющих плоские направляющие линии.
7. В какой последовательности соединяются точки искомой линии пересечения поверхностей, и как определяется ее видимость в проекциях?
8. Какие точки линии пересечения поверхностей называют главными (опорными)?
9. Изложите принципы построения линий пересечения поверхностей вращения между собой.
К теме 10. Плоскости и поверхности, касательные к поверхности
1. Какую плоскость называют касательной к поверхности в данной точке? 2. Что называют нормалью поверхности в данной точке?
3. Докажите, что плоскость, касательная к поверхности вращения в точке, расположенной на главном меридиане, является проецирующей.
К теме 11. Развертки поверхностей
1. Что называют разверткой поверхностей?
2. Какие поверхности называют развертывающимися, какие неразверты-вающимися?
3. Укажите основные свойства разверток.
4. Укажите последовательность графических построений разверток поверхностей конуса и цилиндра.
5. Что называют аппроксимацией поверхности?
К теме 12. Аксонометрические проекции
1. Какие проекции называют аксонометрическими? Назовите их виды.
2. Что называют коэффициентом (показателем) искажения?
3. Что представляет собой треугольник следов?
4. Укажите коэффициенты искажений по направлениям осей в прямоугольной изометрии, диметрии.
5. Укажите направления и величины осей эллипсов как изометрических и диметрических проекций окружностей, вписанных в квадраты граней куба, ребра которого параллельны координатным осям.
ЛИТЕРАТУРА
1. Гордон В.О. Курс начертательной геометрии: учеб. пособие / В.О. Гордон, М.А. Семенцов-Огиевский; под ред. В.О. Гордона, Ю.Б. Иванова. 24-е изд., стереотип. - М.: Высшая школа, 2002.
2. Гордон В.О. Сборник задач по курсу начертательной геометрии: учеб. пособие / В.О. Гордон, Ю. Б. Иванов, Т.Е. Солнцева; под ред. Ю.Б. Иванова. - 8-е изд., стереотип. - М.: Высшая школа, 2002.
3. Виницкий И.Г. Начертательная геометрия: учебник / И.Г. Виницкий. - М.: Высшая школа, 1975.
4. Бубенников А.В. Начертательная геометрия: учебник / А.В. Бубенников. - М.: Высшая школа, 1985.
5. Фролов С.А. Начертательная геометрия: учебник / С.А. Фролов / 2-е изд., перераб. и доп. - М.: Машиностроение, 1983.
6. Локтев О.В. Задачник по начертательной геометрии: учеб. пособие / О.В. Локтев, П.А. Числов. - 4-е изд., стереотип. - М.: Высшая школа, 2002.
7. Локтев О.В. Краткий курс начертательной геометрии: учебник / О.В. Локтев. - 4-е изд., стереотип. - М.: Высшая школа, 2003.
8. Государственные стандарты Единой системы конструкторской документации (ЕСКД).
9. Федоренко В.А. Справочник по машиностроительному черчению: учеб. пособие / В. А. Федоренко, А. И. Шошин. - Л.: Машиностроение, 1983.
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Методические указания и контрольные задания
Составили: Антропова Татьяна Владимировна
Василькова Ирина Анатольевна
Рецензент Е.А. Данилова
Редактор О.А. Луконина
Лицензия ЛР № 020271 от 15.01.96
Подписано в печать Формат 60´ 84 1/16
Бум.тип. Усл.-печ.л. Усл.-изд.л.
Тираж 100 экз. Заказ Бесплатно
Саратовский государственный технический университет
410054 г. Саратов, ул. Политехническая, 77.
Копипринтер СГТУ, 410054 г. Саратов, ул. Политехническая, 77.