Лабораторная работа №3. Освоить математическое программирование, выполнив конкретное задание по определению программ выпуска изделий

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

В МАШИНОСТРОЕНИИ

НА ОСНОВЕ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

ЦЕЛЬ РАБОТЫ

Освоить математическое программирование, выполнив конкретное задание по определению программ выпуска изделий, по «расцеховке» изделий и по рациональному раскрою листового материала. Научиться выполнять решения задач математического программирования в среде MS Excel

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Методы математического программирования представляют собой класс моделей, применяемых для формализации задач планирования, предусматривающих распределение ограниченного количества ресурсов разных видов. Подобного рода задачи решаются в различных отраслях деятельности: в экономике, в промышленности, при разработке проектов, составлении расписаний, планировании военных операций и т.п.

Употребление слова «программирование» связано с тем, что при решении задач находят такой набор переменных, который является программой (планом) при выполнении поставленной задачи. Методы линейного программирования применяются в случае, когда математическая модель изучаемого процесса может быть представлена в виде совокупности линейных отношений. Эти линейные отношения связывают некоторые параметры, определяющие ход процесса, и состоят из системы ограничений и целевой функции.

Методы решения такого типа задач позволяют найти оптимальные варианты управления, процессы, структуры, т.е. выбрать лучшее решение из всех возможных. Такие задачи относятся к задачам оптимизации.

Условно типы задач из области машиностроения можно разделить на технико-экономические, технические, технологические, проектно-организационные, транспортные. Косвенным образом соотносятся с машиностроением и другие типы задач, которые могут быть решены методом линейного программирования: задачи оптимального планирования, распределения различных ресурсов, управления запасами, календарное планировании, межотраслевого баланса и т. п.

В рассматриваемой лабораторной работе требуется составить математическую модель задачи машиностроения, основанной на линейном программировании. Требуется составить целевую функцию, систему ограничений и решить задачу, пользуясь MS EXCEL.

Технико-экономическая задача определения программ выпуска нескольких видов продукции при ограниченности

Сырья

Рассмотрим постановку этой задачи на конкретном примере.

Для изготовления двух видов продукции 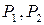используют три вида сырья: 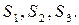Запасы сырья, затрачиваемые на изготовление единицы продукции, а также величина прибыли, получаемая от реализации единицы продукции приведены в табл. 2.1. Необходимо составить такой план выпуска продукции, чтобы при её реализации получить максимальную прибыль.

Таблица 3.1

Исходные данные

Вид сырья	Запасы сырья	Кол-во единиц сырья, идущих на изготовление единицы продукции
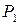
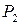
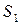
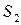
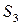
Прибыль от единицы продукции, руб.

Обозначим через количество единиц продукции 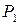, а через 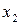количество единиц продукции 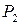. Тогда, учитывая количество единиц сырья, затрачиваемых на изготовление единицы продукции, а также запасы сырья, получим систему ограничений:

, (3.1)

которая показывает, что количество сырья, необходимое на изготовление продукции, не может превысить имеющихся запасов. Кроме того, на неизвестные и 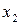должно быть наложено ограничение неотрицательности: 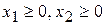(с позиций здравого смысла)

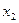Конечную цель решаемой задачи – получение максимальной прибыли при реализации продукции – выразим как функцию двух переменных и . Реализация единиц продукции вида 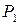и 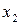единиц продукции вида 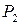дает соответственно 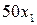и 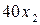руб. прибыли. Выражение для суммарной прибыли есть также выражение для целевой функции задачи

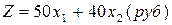. (3.2)

Необходимо найти такие неотрицательные значения и 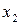, которые удовлетворяли бы системе ограничений (3.1) и при которых функция (3.2) мела бы максимальное значение.