
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методичні вказівки
|
|
Епюри згинальних моментів 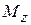 і
і 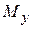 у двох головних взаємно перпендикулярних площинах пропонується будувати окремо. Повний прогин визначається за формулою
у двох головних взаємно перпендикулярних площинах пропонується будувати окремо. Повний прогин визначається за формулою 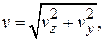 де
де 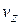 і
і 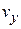 – прогини перерізу балки в напрямках головних осей інерції. На рис. 3 та рис. 4 наведено епюри згинальних моментів, епюри нормальних напружень та приклад визначення повного прогину.
– прогини перерізу балки в напрямках головних осей інерції. На рис. 3 та рис. 4 наведено епюри згинальних моментів, епюри нормальних напружень та приклад визначення повного прогину.
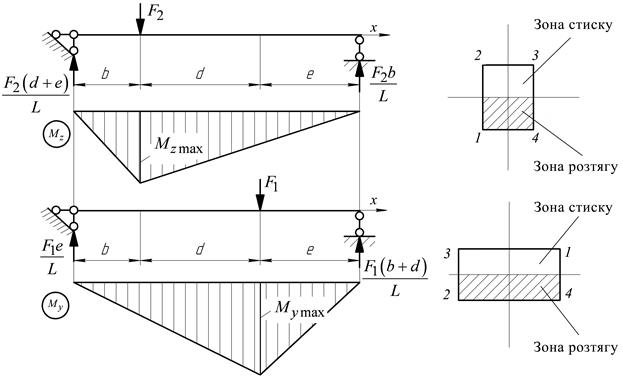
Рис. 3. Епюри згинальних моментів
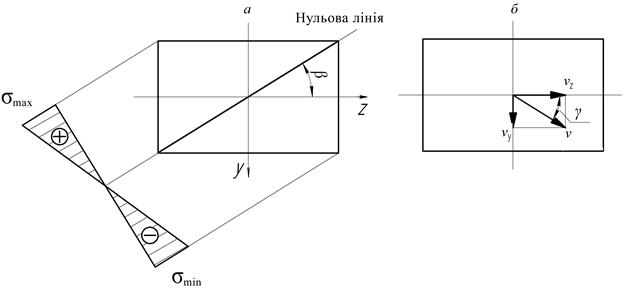
Рис. 4. Епюра нормальних напружень (а) та схема визначення повного прогину (б)
Задача № 9
Розрахунки на міцність при навантаженні позацентровою силою
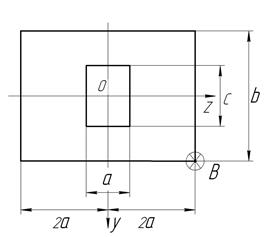
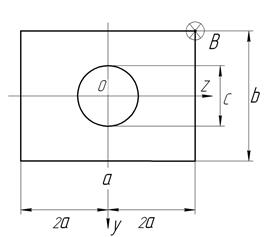
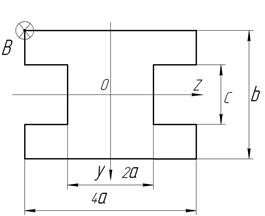
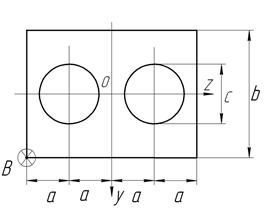
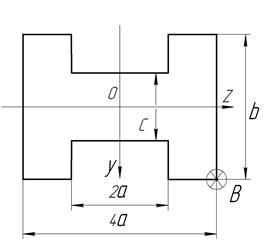
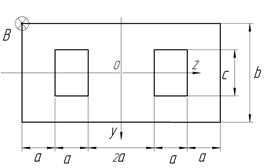
На колону заданого поперечного перерізу в точці В верхнього вільного кінця діє позацентрова сила 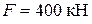 , яка її розтягає (стискає) (рис. 5). Стискальна сила позначається зіркою.
, яка її розтягає (стискає) (рис. 5). Стискальна сила позначається зіркою.
 1 1
|  2 2
|
 3 3
|  4 4
|
 5 5
|  6
6
|
Рис. 5. Варіанти схем поперечних перерізів до задачі № 9
Потрібно:
1. Накреслити поперечний переріз у масштабі.
2. Знайти положення і вказати на рисунку головні центральні осі інерції. Визначити значення головних моментів інерції і головних радіусів інерції перерізу.
3. Визначити значення відрізків, що відсікаються нульовою лінією на осях z та y. Побудувати нульову лінію.
4. Визначити найбільші розтягальні та стискальні напруження і побудувати епюру нормальних напружень.
5. Побудувати ядро перерізу і вказати координати його характерних точок, як зображено в прикладі на рис. 6.
Вихідні дані обрати з табл. 3.
Таблиця 3
Вихідні дані до задачі № 9
| № рядка | Схема за рис. 5 | b, см | с, см | а, см |
| е | б | в | д |
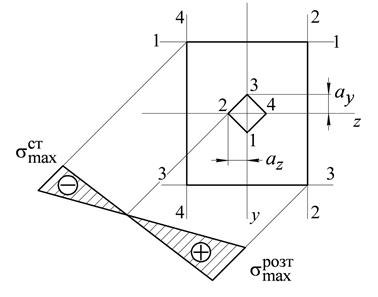
Рис. 6. Приклад епюри нормальних напружень із зображенням ядра перерізу
Задача № 10
Розрахунок на міцність плоско-просторових статично визначуваних
стержневих систем
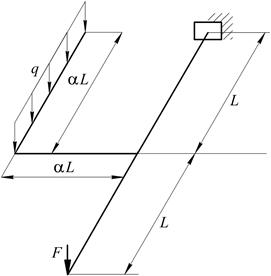
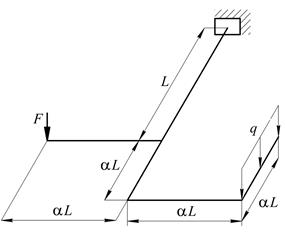
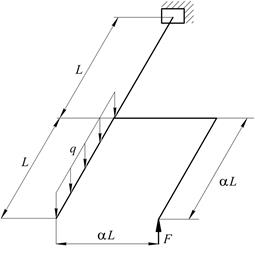
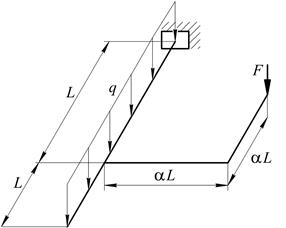
На рис. 7 зображені осі ламаних стержнів круглого поперечного перерізу, які розміщені в горизонтальній площині. На стержневу систему діє навантаження у вертикальній площині. Кути між стержнями в місцях з’єднання прямі.
Потрібно:
1. Побудувати окремо епюри згинальних 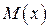 та крутних
та крутних 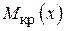 моментів.
моментів.
 1
1
|  2 2
|
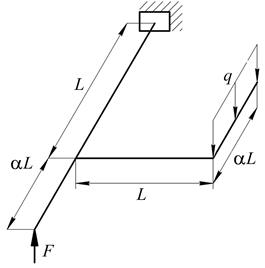
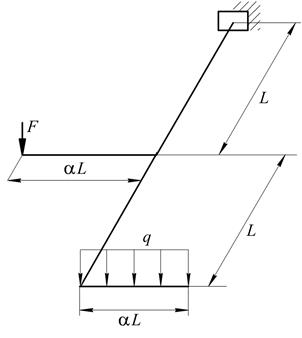
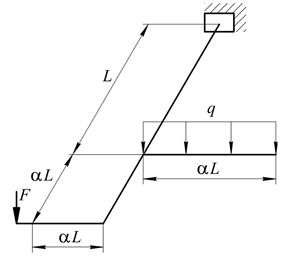
Рис. 7. Варіанти розрахункових схем до задачі № 10 (див. також с. 12)
 3 3
|  4 4
|
 5 5
|  6 6
|
 7
7
| 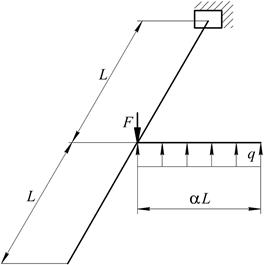 8 8
|
Рис. 7. Варіанти розрахункових схем до задачі № 10 (див. також с. 13)
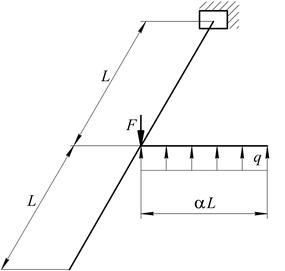
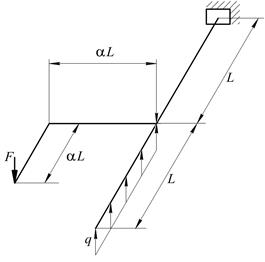
| 
|
Рис. 7. Варіанти розрахункових схем до задачі № 10 (закінчення)
2. Встановити положення небезпечного перерізу і знайти розрахунковий момент за четвертою теорією міцності.
3. Виконати добір діаметра круглого перерізу стержня при розрахунковому опорі 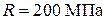 (для студентів будівельних спеціальностей) або при допустимому напруженні
(для студентів будівельних спеціальностей) або при допустимому напруженні 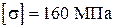 (для студентів усіх інших спеціальностей). Отримане значення діаметра вала округлити до найближчого більшого цілого числа, що є кратним п’яти.
(для студентів усіх інших спеціальностей). Отримане значення діаметра вала округлити до найближчого більшого цілого числа, що є кратним п’яти.
Вихідні дані обрати з табл. 4.
Таблиця 4
Вихідні дані до задачі № 10
| № рядка | Схема за рис. 7 | F, кН | q, кН/м | a | L, м |
| 0, 5 | 1, 0 | ||||
| 0, 6 | 1, 1 | ||||
| 0, 7 | 1, 2 | ||||
| 0, 8 | 1, 3 | ||||
| 0, 9 | 1, 4 | ||||
| 1, 0 | 1, 5 | ||||
| 0, 9 | 1, 4 | ||||
| 0, 8 | 1, 3 | ||||
| 0, 7 | 1, 2 | ||||
| 0, 6 | 1, 1 | ||||
| е | б | в | г | е |
Задача № 11
Розрахунок на міцність валів при одночасній дії згину та кручення
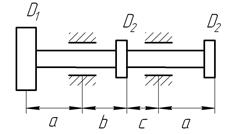
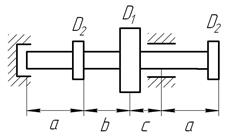
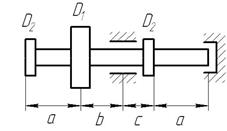
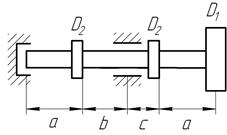
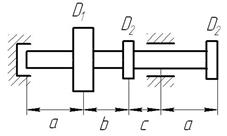
Шків діаметром 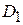 , у якого паски перебувають у горизонтальній площині, робить n обертів за хвилину і передає потужність
, у якого паски перебувають у горизонтальній площині, робить n обертів за хвилину і передає потужність 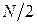 на кожний інший шків діаметром
на кожний інший шків діаметром 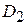 (рис. 8).
(рис. 8).
Потрібно:
1. Визначити крутні моменти, що прикладені до шківів, та побудувати епюру 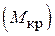 .
.
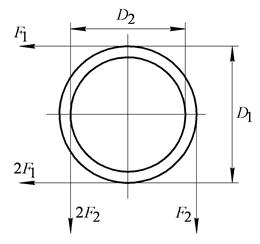
2. Визначити окружні зусилля 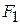 і
і 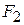 , які діють на шківи, залежно від крутних моментів і діаметрів шківів
, які діють на шківи, залежно від крутних моментів і діаметрів шківів 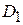 і
і 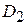 .
.
3. Визначити сили, які згинають вал у вертикальній та горизонтальній площинах, нехтуючи при цьому вагою вала та шківів.
4. Побудувати епюри згинальних моментів у вертикальній та горизонтальній площинах 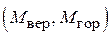 , а також епюру результуючого згинального моменту
, а також епюру результуючого згинального моменту 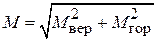 .
.
5. Обрати діаметр вала за третьою теорією міцності. Отримане значення діаметра вала округлити до найближчого більшого цілого числа, що є кратним п’яти.
 1 1
|  2 2
|
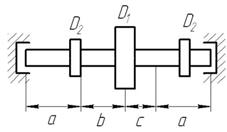
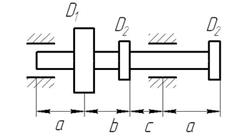
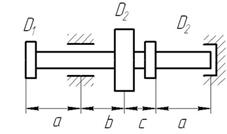
Рис. 8. Варіанти розрахункових схем до задачі № 11 (див. також с. 15)
 3
3
|  4
4
|
 5
5
|  6
6
|
 7
7
|  8
8
|
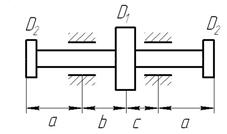 9
9
| 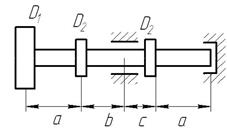 10
10
|
Рис. 8. Варіанти розрахункових схем до задачі № 11 (закінчення)
Слід мати на увазі, що для кожного поперечного перерізу вала є своя площина дії результуючого згинального моменту, але для круглого перерізу можна сполучати площини М для всіх поперечних перерізів. Тому епюру результуючого моменту слід будувати в площині рисунка.
Таблиця 5
Вихідні дані до задачі № 11
| № рядка | Схема за рис. 8 | N, кВт | n, об/хв | а, м | в, м | с, м | D 1, м | D 2, м |
| 1, 1 | 1, 6 | 1, 4 | 0, 6 | 0, 4 | ||||
| 1, 2 | 1, 6 | 1, 5 | 0, 8 | 0, 6 | ||||
| 1, 3 | 1, 4 | 1, 6 | 1, 0 | 0, 8 | ||||
| 1, 4 | 1, 3 | 1, 5 | 1, 0 | 0, 6 | ||||
| 1, 5 | 1, 2 | 1, 4 | 0, 8 | 0, 4 | ||||
| 1, 6 | 1, 1 | 1, 3 | 0, 6 | 0, 6 | ||||
| 1, 5 | 1, 2 | 1, 2 | 0, 8 | 0, 4 | ||||
| 1, 4 | 1, 3 | 1, 3 | 1, 0 | 0, 6 | ||||
| 1, 3 | 1, 4 | 1, 4 | 1, 0 | 0, 8 | ||||
| 1, 2 | 1, 5 | 1, 3 | 0, 8 | 0, 6 | ||||
| е | а | б | в | г | д | е | б |
Задача № 12
Добір площі поперечного перерізу стиснутого стержня
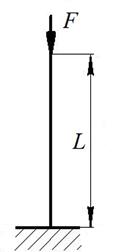
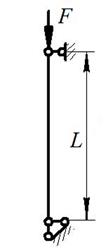
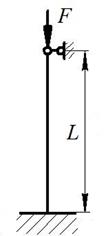
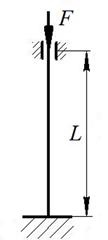
Сталевий стержень довжиною L стискається силою F (рис. 9).
Потрібно:
1. Виконати добір елементів перерізу з умови стійкості при розрахунковому опорі 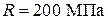 (для студентів будівельних спеціальностей) або при допустимому напруженні
(для студентів будівельних спеціальностей) або при допустимому напруженні 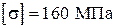 (для студентів усіх інших спеціальностей). Розрахунок виконати послідовним наближенням, попередньо задавшись коефіцієнтом
(для студентів усіх інших спеціальностей). Розрахунок виконати послідовним наближенням, попередньо задавшись коефіцієнтом 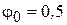 .
.
2. Визначити критичну силу та коефіцієнт запасу стійкості.
Вихідні дані обрати з табл. 6.
Таблиця 6
Вихідні дані до задачі № 12
| № рядка | F, кН | L, м | Схема закріплення стержня (рис. 9) | Форма перерізу стержня (рис. 10) |
| 2, 4 | ||||
| 2, 3 | ||||
| 2, 2 | ||||
| 2, 1 | ||||
| 2, 0 | ||||
| 2, 1 | ||||
| 2, 2 | ||||
| 2, 3 | ||||
| 2, 4 | ||||
| 2, 5 | ||||
| б | в | д | е |
 1
1
|  2
2
|  3
3
|  4
4
|
Рис. 9. Варіанти розрахункових схем до задачі № 12
 1
1
|  2
2
|
 3
3
|  4
4
|
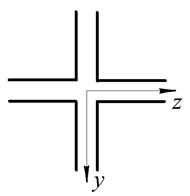
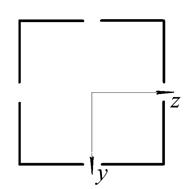
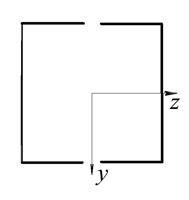
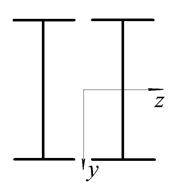
Рис. 10. Варіанти поперечних перерізів до задачі № 12
Задача № 13
Розрахунки на міцність та жорсткість балок при змушених коливаннях як систем з одним степенем вільності
На балках (рис. 11) встановлено двигун вагою 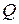 , який робить
, який робить 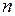 обертів за хвилину. Поперечний переріз балки складається із двох двотаврів. Відцентрова сила інерції, що виникає внаслідок незрівноваженості обертових частин двигуна, визначається за формулою
обертів за хвилину. Поперечний переріз балки складається із двох двотаврів. Відцентрова сила інерції, що виникає внаслідок незрівноваженості обертових частин двигуна, визначається за формулою
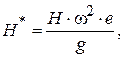
де 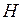 – незрівноважена маса,
– незрівноважена маса,
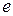 – ексцентриситет.
– ексцентриситет.
У розрахунках слід нехтувати власною вагою балки й силами опору під час коливань.
Потрібно:
1. Визначити частоту власних коливань 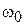 .
.
2. Визначити частоту збурюючої сили 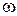 .
.
3. Визначити коефіцієнт наростання коливань.
Коефіцієнт наростання коливань визначається за формулою
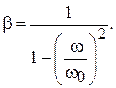
У розрахунках 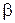 слід приймати додатньою величиною незалежно від знака знаменника.
слід приймати додатньою величиною незалежно від знака знаменника.
4. Визначити динамічний коефіцієнт за формулою
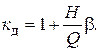
5. Визначити найбільше нормальне напруження
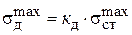
та найбільший динамічний прогин
Вихідні дані обрати з табл. 7.
Таблиця 7
Вихідні дані до задачі № 13
| № рядка | Схема за рис. 11 | № двотавра | L, м | Q, кН | Незрівноважена маса H, т | Ексцентриситет e, см | n, об/хв |
| 2, 6 | 0, 20 | ||||||
| 2, 4 | 0, 24 | ||||||
| 2, 2 | 0, 30 | ||||||
| 2, 0 | 0, 30 | ||||||
| 2, 0 | 0, 26 | ||||||
| 1, 8 | 0, 24 | ||||||
| 1, 8 | 0, 22 | ||||||
| 2, 2 | 0, 20 | ||||||
| 2, 4 | 0, 18 | ||||||
| 2, 6 | 0, 16 | ||||||
| е | б | в | д | д | е | в |

| − поперечний переріз балки. |
 1 1
|  2 2
|
 3 3
|  4 4
|
 5 5
|  6 6
|
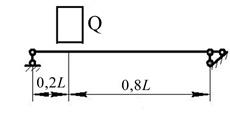
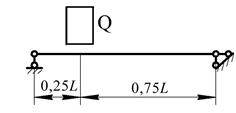
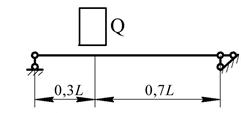
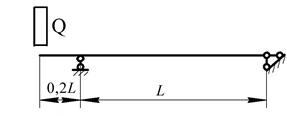
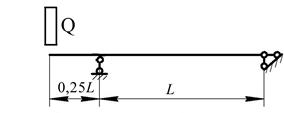
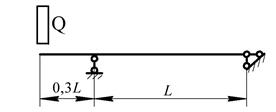
Рис. 11. Варіанти розрахункових схем до задачі № 13
Задача № 14
Розрахунки на міцність при напруженнях, які змінюються в часі
У небезпечному перерізі вала діаметром d діють крутний момент T та згинальний момент M. Вал зроблено з вуглецевої сталі, у якої границя міцності 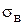 і границя текучості
і границя текучості 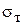 ; вал не має різких переходів, виточок, канавок, його поверхня чисто оброблена різцем.
; вал не має різких переходів, виточок, канавок, його поверхня чисто оброблена різцем.
Визначити коефіцієнт запасу міцності стосовно руйнування від утомленості, приймаючи нормальні напруження як такі, що змінюються за симетричним циклом, а дотичні напруження – за пульсуючим (віднульовим) циклом.
Масштабні коефіцієнти концентрації для нормальних і дотичних напружень можна приймати однаковими. Вихідні дані обрати з табл. 8.
Для вуглецевої сталі значення коефіцієнтів, що характеризують чутливість до асиметрії циклів приймати рівними: 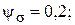
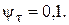
Потрібно:
1. Визначити максимальні нормальні та дотичні напруження.
2. Визначити границю текучості при крученні 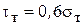 та границю витривалості при згинанні та крученні
та границю витривалості при згинанні та крученні 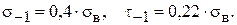
3. Знайти дійсний коефіцієнт концентрації напружень за формулою 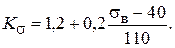
4. Визначити масштабний коефіцієнт 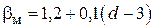 , де d – діаметр вала, см.
, де d – діаметр вала, см.
5. Знайти коефіцієнти запасу міцності за нормальними та дотичними напруженнями.
6. Визначити загальні результуючі коефіцієнти запасу міцності текучості та руйнування від утомленості.
Таблиця 8
Вихідні дані до задачі № 14
| № рядка | d, мм | М, кН·м | Т, кН·м | 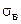 , МПа , МПа
| 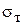 , МПа , МПа
|
| 0, 20 | 0, 30 | ||||
| 0, 25 | 0, 35 | ||||
| 0, 30 | 0, 40 | ||||
| 0, 35 | 0, 45 | ||||
| 0, 40 | 0, 50 | ||||
| 0, 45 | 0, 55 | ||||
| 0, 50 | 0, 60 | ||||
| 0, 45 | 0, 55 | ||||
| 0, 40 | 0, 50 | ||||
| 0, 35 | 0, 45 | ||||
| е | б | в | д | г |
ПРИКЛАДИ РОЗВ’ЯЗАННЯ ЗАДАЧ
Задача № 8
Розрахунки на міцність та жорсткість балки при згині
у двох головних площинах
Вихідні дані:
схема – 2 (рис. 12, а); довжина прогону L =3, 2 м; навантаження: 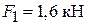 ,
, 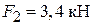 ; форма перерізу – 2 (рис. 12, б); геометричні розміри перерізу:
; форма перерізу – 2 (рис. 12, б); геометричні розміри перерізу: 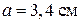 ,
, 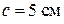 .
.
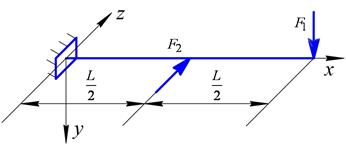 а
а
| 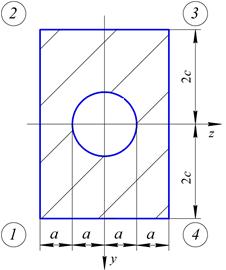 б б
|
Рис. 12. Розрахункова схема балки (а) та схема поперечного перерізу (б)