Розв’язання. Розрахунки виконуємо методом послідовних наближень.

Розрахунки виконуємо методом послідовних наближень.

Використаємо умову стійкості:

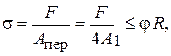
де 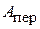– площа перерізу;

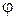– коефіцієнт зменшення розрахункового опору;

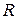– розрахунковий опір.

Визначимо площу поперечного перерізу одного кутика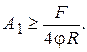

Виконаємо нульове наближення, приймаючи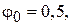

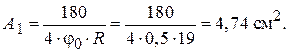
За сортаментом з табл. Д.2 обираємо кутик 65´ 40´ 5 з такими геометричними характеристиками: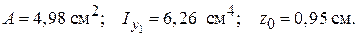

Визначимо мінімальний радіус інерції за формулою:

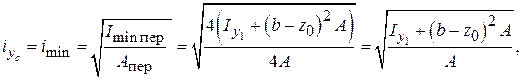
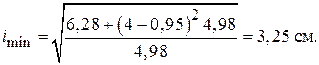
Знайдемо гнучкість стержня: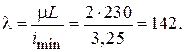

За табл. Д.5 значень 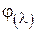визначимо коефіцієнт зменшення основного розрахункового опору: гнучкість 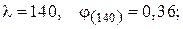гнучкість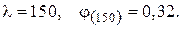

За формулою лінійної інтерполяції визначимо коефіцієнт зменшення розрахункового опору для гнучкості :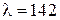

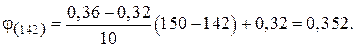
Визначимо дійсне напруження

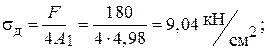
та допустиме напруження на стійкість

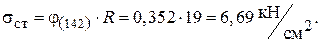
Стержень перевантажено на 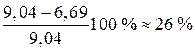, тому покращимо добір перерізу шляхом збільшення площі перерізу й зробимо таке наближення.

I наближення. Коефіцієнт зменшення розрахункового опору:

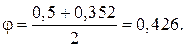
Площа поперечного перерізу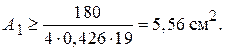

За сортаментом табл. Д.1 обираємо кутик, близький за значенням до площі поперечного перерізу, а саме кутик 70´ 45´ 5 з геометричними характеристиками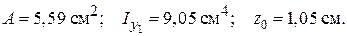

Мінімальний радіус інерції:

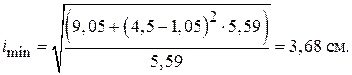
Визначимо гнучкість стержня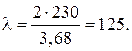

За табл. Д. 5 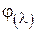значень обираємо: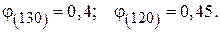

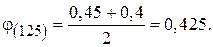
Перевірка напружень:

дійсне напруження

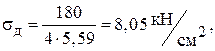
допустиме напруження на стійкість

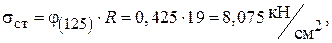
Стержень недовантажено на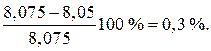

Остаточно приймаємо кутик 70´ 45´ 5 з площею поперечного перерізу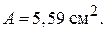

Визначаємо критичну силу:

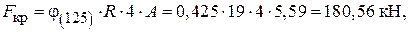
тоді коефіцієнт запасу стійкості дорівнює:

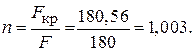
Задача № 13

Розрахунки на міцність та жорсткість балок при змушених коливаннях
як систем з одним степенем вільності

Вихідні дані:

схема – 2; балка складається із двох двотаврів № 24 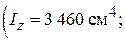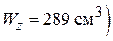, довжина балки ; вага двигуна 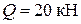та величина незрівноваженої маси 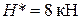; ексцентриситет 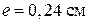; частота обертання ротора двигуна .

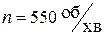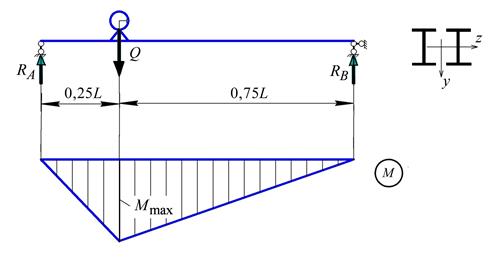
Рис. 25. Розрахункова схема та епюра згинальних моментів