
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вибір приладів для вимірювань
|
|
Вибір границі вимірювання приладів. Вибір того чи іншого приладу для конкретного вимірювання, крім економічних факторів (вартість приладів та їх обслуговування), залежить від орієнтовного значення вимірювання (струму чи напруги), потрібного часу вимірювання, необхідної точності вимірювання, а також інших факторів, наприклад, можливості автоматизованого опрацювання результатів вимірювання за допомогою комп’ютера.
Орієнтовне значення вимірюваної величини впливає на вибір границь вимірювання приладу. Очевидно, що границя вимірювання приладу повинна бути не меншою від значення вимірюваної величини. Тому перед вимірюванням експериментатор повинен оцінити орієнтовне значення вимірюваної напруги чи струму, наприклад, шляхом спрощених розрахунків на основі відомих параметрів об’єкта дослідження.
Клас точності приладу. Похибки приладу. Інша характеристики, що впливає на вибір приладів, це необхідна точність вимірювання.
Узагальненою характеристикою точності приладу є його клас точності, згідно з яким встановлюються границі основних та додаткових похибок. Ці границі можуть встановлюватися у формах абсолютної, відносної чи зведеної похибок.
Абсолютна похибка Δ х приладу – це різниця між показом приладу хп та істинним значенням Х вимірюваної величини:
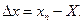 (1.1)
(1.1)
Відносна похибка приладу – відношення абсолютної похибки до істинного значення. Відносна похибка, як правило, виражається у відсотках:
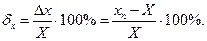 (1.2)
(1.2)
Зведена похибка γ приладу – це виражене у відсотках відношення абсолютної похибки до нормувального значення хN (умовно прийнятого значення, що для різних приладів може дорівнювати верхній границі вимірювання хК (кінець шкали), діапазону вимірювання, довжині шкали, тощо):
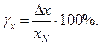 (1.3)
(1.3)
Клас точності аналогових вимірювальних приладів. Для аналогових амперметрів та вольтметрів клас точності найчастіше встановлює границі γ гр зведеної похибки. При чому γ гр вибране з ряду (1; 1.5; 2; 2.5; 4; 5; 6)·10n, %, де n = 1, 0, -1, -2, … Фактичне значення зведеної похибки приладу повинне знаходитись в межах допустимих значень, що задаються класом точності, тобто:
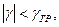 чи
чи 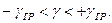 (1.4)
(1.4)
Наприклад, при класі точності 0.5 границі допустимої зведеної похибки γ гр = ±0.5 %, чи -0.5 % ≤ γ ≤ 0.5 %.
За відомими границями зведеної похибки, відповідно до означення зведеної похибки, можна визначити допустимі границі абсолютної та відносної похибок:
абсолютної
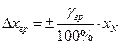 ; (1.5)
; (1.5)
відносної
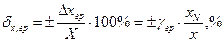 . (1.6)
. (1.6)
Таким чином, якщо клас точності приладу встановлений у формі зведеної похибки, то граничне значення абсолютної похибки (1.5) є сталим (не залежить від значення вимірюваної величини). Граничне значення відносної похибки (1.6) зростає зі зменшенням вимірюваної величини, тобто точність вимірювань зменшуватиметься, якщо показ приладу буде значно меншим за границю вимірювання.
Провівши вимірювання, за показом приладу хп отримуємо оцінку вимірюваної величини, істинне значення Х якої накривається інтервалом навколо показу хп ширина якого визначається межами допустимої похибки ±Δ гр, тобто:
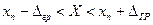 . (1.7)
. (1.7)
Тому на практиці при обчисленні граничного значення відносної похибки в (1.6), враховуючи близькість Х та хп, замість істинного значення Х використовують показ приладу хп:
 . (1.8)
. (1.8)
Приклад 1.1.Розглянемо приклад. Нехай здійснено вимірювання аналоговим вольтметром з верхньою границею вимірювання Uк = 150 В та класом точності 0.2 і отримано показ Uп = 120.0 В. Необхідно оцінити границі абсолютної та відносної похибок.
Оскільки клас точності для аналогових вольтметрів встановлює границі зведеної похибки (γ гр = ±0.2%), то при нормувальному значенні, що дорівнює верхній границі вимірювання UN = Uк = 150 В, границі абсолютної похибки згідно з (1.5) становлять:
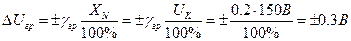 .
Отже, -0.3 В ≤ Δ Uгр ≤ 0.3 В, а істинне значення напруги знаходиться в межах: .
Отже, -0.3 В ≤ Δ Uгр ≤ 0.3 В, а істинне значення напруги знаходиться в межах:
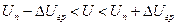 , чи
119.7 (В) ≤ 120.3 (В) або U = (120.0 ± 0.3) В.
Границі відносної похибки згідно з (1.8) становлять , чи
119.7 (В) ≤ 120.3 (В) або U = (120.0 ± 0.3) В.
Границі відносної похибки згідно з (1.8) становлять
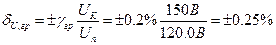 .
Тобто -0.25 % ≤ δ U, гр ≤ 0.25 %. .
Тобто -0.25 % ≤ δ U, гр ≤ 0.25 %.
|
Клас точності цифрових вимірювальних приладів. Клас точності цифрових приладів встановлює границі основної допустимої відносної похибки за двочленною формулою:
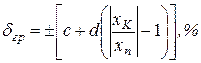 , (1.9)
, (1.9)
тут коефіцієнти c і d мають значення з вказаного вище ряду, причому с – це граничне значення відносної похибки в кінці шкали, коли хп = хК, а коефіцієнт d – це граничне значення зведеної похибки на початку шкали, коли хп = 0.
Границі абсолютної похибки визначають в цьому випадку за попередньо обчисленою граничною відносною похибкою δ х, гр або використовуючи (1.9), тобто за формулами:
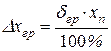 ; або
; або 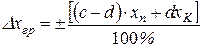 . (1.10)
. (1.10)
Приклад 1.2.Наприклад, на границі вимірювання ІК = 100 мА отримаємо показ амперметра І = 50.14 мА. Необхідно оцінити границі відносної та абсолютної похибки, якщо клас точності амперметра c/d = 0.1/0.05.
Границі відносної похибки знайдемо за формулою (1.9):
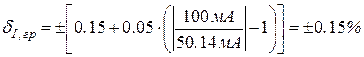 ,
і абсолютної – за (1.10): ,
і абсолютної – за (1.10):
 .
Зауважимо, що згідно з (1.10), границі абсолютної похибки лінійно зростають зі значенням вимірюваної величини. .
Зауважимо, що згідно з (1.10), границі абсолютної похибки лінійно зростають зі значенням вимірюваної величини.
|