Основное уравнение МКТ газа

Основное уравнение МКТ связывает микропараметры частиц (массу молекулы, среднюю кинетическую энергию молекул, средний квадрат скорости молекул) с макропараметрами газа (р - давление, V - объем, Т - температура).

Давление газа на стенки сосуда пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.

Ниже приведены различные выражения для основного уравнения МКТ:

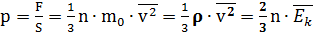
где

р - давление газа на стенки сосуда(Па)

n - концентрация молекул, т.е. число молекул в единице объема (1/м3)
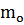- масса молекулы (кг)
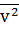- средний квадрат скорости молекул (м2/с2)

ρ - плотность газа (кг/м3)
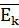- средняя кинетическая энергия молекул (Дж)

Давление идеального газа на стенки сосуда зависит от концентрации молекул и пропорционально средней кинетической энергии молекул.

Средняя квадратичная скорость молекул — среднее квадратическое значение модулей скоростей всех молекул рассматриваемого количества газа

Для того чтоб понять, откуда же у нас получается эта формула, мы выведем среднюю квадратичную скорость молекул. Вывод формулы начинается с основного уравнения молекулярно кинетический теории (МКТ):

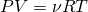
Где 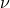у нас количество вещества, для более легкого доказательства, возьмем на рассмотрение 1 моль вещества, тогда у нас получается:

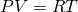
Если посмотреть, то PV это две третьих средней кинетической энергии всех молекул (а у нас взят 1 моль молекул):

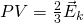
Тогда, если приравнять правые части, у нас получается, что для 1 моля газа средняя кинетическая энергия будет равняться:

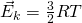
Но средняя кинетическая энергия, так же находится, как:

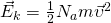
А вот теперь, если мы приравняем правые части и выразим из них скорость и возьмем квадрат, Число Авогадро на массу молекулы, получается Молярная масса 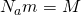то у нас и получится формула для средней квадратичной скорости молекулы газа:

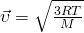
А если расписать универсальную газовую постоянную, как 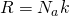, и за одно молярную массу 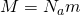, то у нас получится?

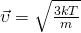
В Формуле мы использовали:

— Средняя квадратичная скорость молекул

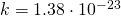— Постоянная Больцмана

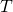— Температура

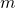— Масса одной молекулы

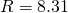— Универсальная газовая постоянная

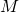— Молярная масса

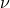— Количество вещества

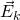— Средняя кинетическая энергия молекул

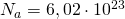— Число Авогадро

Вопрос 14:

Барометрическая формула— определяет зависимость давления или плотности газа от высоты в поле тяжести

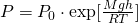
Давайте теперь узнаем, откуда же получается барометрическая формула. Давление газа на некой высоте, определяется как:

Теперь возьмем колонну в атмосфере и выделим в ней тонкий слой воздуха высотой dh. Ясно, что такой слой вызывает изменение давления на величину dP:

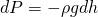
Знак минус необходим для того, что с увеличением высоты давление уменьшается

Рассматривая атмосферный воздух как идеальный газ, можно воспользоваться уравнением Менделеева — Клапейрона

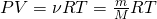
Из этого уравнения выражаем давление

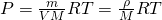
А теперь можно и плотность газа

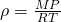
Подставляя найденную плотность газа в дифференциальное уравнение dP, мы получаем:

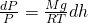
Сделав все преобразования. мы получаем зависимость давления P от высоты подъема h. Теперь необходимо проинтегрировать обе части нашего уравнения:

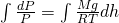
Проинтегрировав, у нас полечилась вот такое уравнение:

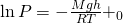
И теперь последний рывок, это взять логарифм. И у нас получится Барометрическое уравнение.

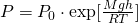
В Формуле мы использовали:

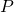— Давление газа (атмосферное)

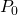— Давление газа над уровнем моря

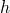— Высота над уровнем моря

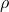— Плотность газа

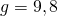— Ускорение свободного падения

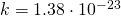— Постоянная Больцмана

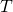— Температура

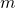— Масса одной молекулы

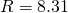— Универсальная газовая постоянная

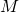— Молярная масса

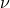— Количество вещества

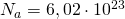— Число Авогадро

Максвелла распределение

Ма́ ксвелла распределе́ ние, распределение по скоростям частиц (молекул) макроскопической физической системы, находящейся в состоянии термодинамического равновесия, (в отсутствии внешнего поля, при условии, что движение частиц подчиняется законам классической механики. Установлено Дж. К. Максвеллом в 1859.

Закон Максвелла о распределении молекул идеального газа по скоростям основан на предположениях, что газ состоит из большого числа N одинаковых молекул, его температура постоянна, а молекулы совершают тепловое хаотическое движение. При этом на газ не действуют силовые поля.

Функция распределения молекул по скоростям f(v)=dN(v)/Ndv определяет относительное число молекул dN(v)/N, скорости которых лежат в интервале от v до v+dv и имеет смысл плотности вероятности.

Для газа, подчиняющегося классической механике, в состоянии статистического равновесия функция распределения f Максвелла по скоростям имеет вид:

f(v) =n(m/2pkT)^3/2exp(-mv²/2kT),

Где m — масса молекулы, Т — абсолютная температура системы, k — постоянная Больцмана.

Значение функции распределения f(v) зависит от рода газа (от массы молекул) и от температуры.

С помощью распределения Максвелла можно вычислять средние значения скоростей молекул и любых функций этих скоростей. В частности, средняя квадратичная скорость v² =3kT/m, а средняя скорость молекулы v = (8kT/pm)^1/2.

Распределение Максвелла не зависит от взаимодействия между молекулами и справедливо не только для газов, но и для жидкостей, если для них возможно применить классическое описание.

Распределение Максвелла вытекает из Гиббса распределения канонического в том случае, когда поступательное движение частиц можно рассматривать в классическом приближении, учитывая, что распределение по скоростям не зависит от распределения по пространственным координатам. Распределение Максвелла является частным решением кинетического уравнения Больцмана для случая статистического равновесия в отсутствии внешних полей. Распределение Максвелла не зависит от характера взаимодействия частиц системы и от внешних сил и потому справедливо как для молекул газа, так и для молекул жидкостей и твердых тел. Распределение Максвелла справедливо также для случая броуновского движения частиц, взвешенных в газе или жидкости.

Вопрос 15: