Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Преобразованные исходные данные
|
|
| Альтернативы, (рынки) Аi | Цели (критерии) | ||
| f 1 | f 2 | f 3 | |
| А1 | -0, 5 | 0, 5 | |
| А2 | 0, 5 | ||
| А3 | -1 | ||
| А4 | -0, 25 | 0, 5 | 0, 3 |
Решение
1. Метод равномерной оптимальности. В соответствии с (1) имеем:
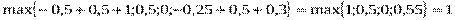
Следовательно, согласно принципу равномерной оптимальности предприятию выгоднее работать на рынке А1.
2. Метод справедливого компромисса. Чтобы воспользоваться данным методом, избавимся от отрицательности критерия f 1, добавив константу, например 1. Тогда значения первого критерия будут равны:
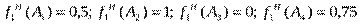
На основании (2) имеем:
mах{0, 5 х 0, 5 х1; 1 х 0 х 0, 5; 0; 0, 75 x 0, 5 х 0, 3}=mах{0, 25; 0; 0; 0, 1125}= 0, 25.
Результат получился аналогичный предыдущему, а именно выгоднее работать на рынке А 1.
3. Метод свертывания критериев. Сначала назначим следующие значения весовых коэффициентов: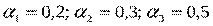 
.Тогда функции свертки в соответствии с (6.3) будут равны:
f 1= -0, 5х0, 2+0, 5х0, 3+1 х 0, 5= 0, 55;
f 2= 0х0, 2+0х0, 3+0, 5х0, 5=0, 25;
f 3= -1х0, 2+1х0, 3+0х0, 5=-0, 2 + 0, 3+0=0, 1;
f 4= -0, 25х0, 2+ 0, 5х0, 3 + 0, 3х0, 5= 0, 25;
mах{ 0, 55; 0, 25; 0, 1; 0, 25} = 0, 55.
При таком значении коэффициентов значимости критериев выгоднее работать на рынке A1.
Если назначить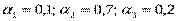 
, то получим:
f 1= -0, 5х0, 1+0, 5х0, 7+1х0, 2= 0, 5;
f 2= 0х0, 1+0х0, 7+0, 5х0, 2=0, 1;
f 3= -1х0, 1+1х0, 7+0х0, 2=0, 6;
f 4= -0, 25х0, 1+ 0, 5х0, 7 + 0, 3х0, 2= 0, 385;
mах{ 0, 5; 0, 1; 0, 6; 0, 385} = 0, 6.
Таким образом, если приоритет отдается доле рынка (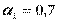
), то фирме имеет смысл работать на рынке А3.
Если же фирма находится в затруднительном положении с точки зрения средств, выделяемых на рекламу, другими словами, для нее в данный момент самым важным является минимизация затрат на рекламу, то коэффициенты значимости могут быть, например, выбраны такие: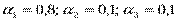 
; mах {-0, 25; 0, 05; -0, 7; -0, 12}=0, 05.
Следовательно, в такой ситуации лучше всего работать на рынке А2.
4. Метод главного критерия. Пусть главный критерий f 1 - затраты на рекламу.
Тогда минимальное значение главного критерия f 1 равно 5 тыс.ден.ед. и соответствует альтернативе А2 .
5. Метод идеальной точки. Определим сначала максимальные значения критериев. А именно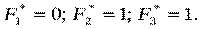 
Матрица отклонений значений критериев от наилучших значений имеет вид: