Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод минимаксного сожаления (метод Сэвиджа).
|
|
Метод характеризует те потенциальные потери, которые фирма будет иметь, если выберет неоптимальное решение.
1. Для каждого состояния внешней среды по конкретной альтернативе определяется максимальное значение функции полезности:
max { eij }
2. По каждой альтернативе рассчитывается показатель: ω { eij }= max { eij }- eij
3. Строится матрица потерь (или матрицу сожалений), затем выбирается альтернатива с наименьшим показателем риска:
e (А*) =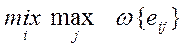 
Рассматривая исходные данные:
| Z1 | Z2 | Z3 | Z4 | |
| А1 | ||||
| А2 | ||||
| А3 |
max { Z1 }= max {530, 490, 575}=575
max { Z2 }= 460
max { Z3 }= 300
max { Z4 }= 270
Матрица потенциальных потерь ω { eij }= max { eij }- eij
| Z1 | Z2 | Z3 | Z4 | |
| А1 | ||||
| А2 | ||||
| А3 |
ω { А1 }= max { 45, 0, 60, 50}=60
ω { А2}= 85
ω { А3}= 80
Оптимальной будет та альтернатива, которая имеет минимальные потери:
e (А*) =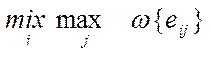 
min { 60, 85, 80} = 60
Следовательно, e (А*) = e (А1), т.е.А1 - имеет минимальные потери выгоды.
4. Метод Лапласа – применяется, когда вероятность состояний внешней среды неизвестны.
Решающее правило: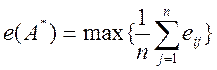 
В рассматриваемом примере:
e (А1) =(530+460+240+220)/4=362, 5
e (А2) =362, 5
e (А3) =361, 25
e (А*) = max { 362, 5; 362, 5; 361, 25 }=362, 5
Следовательно, e (А*) = e (А1) и e (А2)
5. Метод Гурвица. Данный метод представляет собой комбинацию метода максимина и максимакса.
e (А*) =max { α min eij + (1- α) max eij }
α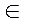 
[0, 1] - вероятность того, что внешняя середа находится в самом невыгодном состоянии, чем опаснее ситуация, тем α → 1
В зависимости от значения весового коэффициента α можно получит различные предпочтительные альтернативы.
Причем, если α =0 – имеем принцип оптимизма, если α =1 – принцип гарантированного результата.
Рассматривая исходные данные: Пусть α =0, 7
| Z1 | Z2 | Z3 | Z4 | |
| А1 | ||||
| А2 | ||||
| А3 |
Тогда, e (А1) =0, 7*220+0, 3*530=313
e (А2) =0, 7*270+0, 3*490=336
e (А3) =0, 7*190+0, 3*575=305, 5
e (А*) =max { 313, 336, 305, 5 }=336, тогда e (А*) = e (А2)
6. Метод Байеса. Метод базируется на использовании вероятностных мер в качестве критерии выбора.
e (А*) =max { eij }= max {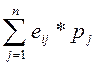 
}
где pj – субъективные вероятности состояния внешней среды; ∑ pj =1
В рассм. примере: пусть p1=0, 4 p2=0, 2 p3=0, 1 p4=0, 3
| Z1 | Z2 | Z3 | Z4 | |
| А1 | ||||
| А2 | ||||
| А3 |
Тогда, e (А1)=530*0, 4+460*0, 2+240*0, 1+220*0, 3=394
e (А2)=385
e (А3)=397
max { 394, 385, 397 }=397, тогда e (А*) = e (min eij)= e (А3)