
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Принятие управленческих решений в условиях неопределенности и риска.
|
|
Большинство задач управления зависит от ряда неизвестных заранее и неуправляемых факторов. Эти задачи обладают той или иной степенью неопределенности, которая может быть как объективной, так и субъективной. В таких задачах неизвестно распределение вероятностей p(Zj), с которыми внешняя среда может находиться в одном из возможных состояний 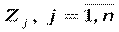 . В этом случае выдвигаются только определенные гипотезы относительно состояний внешней среды.
. В этом случае выдвигаются только определенные гипотезы относительно состояний внешней среды.
Таким образом, в условиях неопределенности и невозможности получения дополнительной информации о неопределенных факторах, элементами описания ситуации планирования являются:
· множество допустимых альтернатив А={A1, A2, …, Am};
· множество возможных состояний внешней среды (множество гипотез) Z={Z1, Z2, …, Zm}.
Каждой реализуемой альтернативе 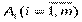 соответствуют некоторые состояния окружающей среды
соответствуют некоторые состояния окружающей среды  . Ожидаемый результат eij (см. табл. 1) при выборе альтернативы Ai и принятии гипотезы Zj получается, если применить функцию предпочтения, или, как чаще всего говорят, функцию полезности f, т.е.:
. Ожидаемый результат eij (см. табл. 1) при выборе альтернативы Ai и принятии гипотезы Zj получается, если применить функцию предпочтения, или, как чаще всего говорят, функцию полезности f, т.е.:
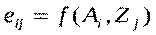
Для выбора лучшей альтернативы имеется ряд специальных методов, ориентированных на использование в условиях неопределенности, которые рассмотрены ниже.
Рассмотрим пример:
Ожидаемые значения прибыли (тыс.грн.) для трех товарных рынков
| Возможные новые товарные рынки | Политическая обстановка | |||
| стабильная | стабильная | нестабильная | нетабильная | |
| Степень конкуренции | ||||
| слабая, Z1 | сильная, Z2 | слабая, Z3 | сильная, Z4 | |
| РынокА1 | ||||
| Рынок А2 | ||||
| Рынок А3 |
1. Метод максимина (принцип гарантированного результата, или метод Вальда)
Данный принцип заключается в выборе в качестве оптимальной (наиболее эффективной) той альтернативы, которая имеет наибольшее среди наименее благоприятных состояний внешней среды значение функции полезности.
Оптимальной считается альтернатива А*, для которой выполняется соотношение:
e (А*) = 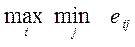
Сначала для каждой альтернативы выбирает минимальное значение функции полезности:
min { А1 } = min { 530, 460, 240, 220 }=220
min { А2 } = 270
min { А3 } = 190
Далее из полученных минимальных значений выбирается максимальное (т.е. «лучшее из худших):
max { 220, 270, 190 } = 270 (для i=2) 336 e (А*) = e (А2)
Следовательн о, оптимальной по методу максимина является альтернатива А2, т.е. фирме целесообразно выходить на рынок А2. Эта самая осторожная альтернатива, так как при любом состоянии внешней среды фирма получит прибыль не менее 270 тыс.грн.
2. Метод максимакса (принцип оптимизма). Метод оптимизма предполагает получение максимального уровня желательности результата. Оптимальная альтернатива выбирается исходя из выражения:
e (А*) = 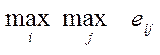
Рассматривая исходные данные:
| А1 | ||||
| А2 | ||||
| А3 |
max { А1 } = max {530, 460, 240, 220}=530
max { А2 } = 490
max { А3 } = 575
max {530, 490, 575} = 575
e (А*) = e (А3) =575 тыс.грн.