З а д а ч а 18

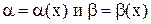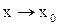Две бесконечно малые функции при или 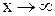называются эквивалентными, если предел их отношения равен единице. Эквивалентность бесконечно малых функций записывается в виде ~ .

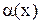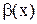Таким образом, если 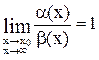, то ~ .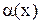

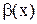Таблица эквивалентных бесконечно малых функций

~ .

~ .

~

~ .

~ .

~ .

~ .

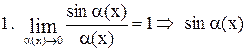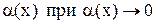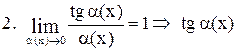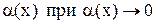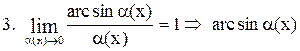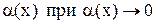
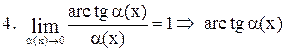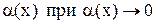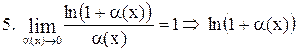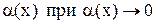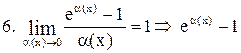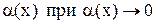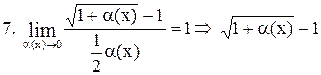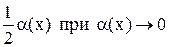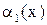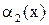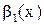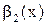Теорема. Предел отношения двух бесконечно малых не изменится, если одну или обе бесконечно малые заменить им эквивалентными, т. е. если ~ и ~ , то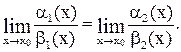

Заметим, что с помощью эквивалентных бесконечно малых раскрывают неопределенность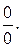

Пример 18

Вычислить предел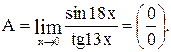

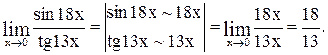
Пример 19

Вычислить предел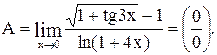

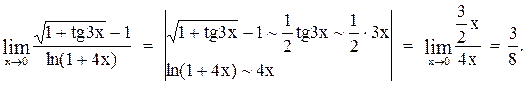
Пример 20

Вычислить предел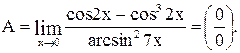

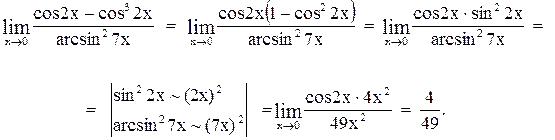
Контрольные варианты к задаче 18

Вычислить пределы функций:

.	.
	.
.	.
.	.
	.
.	.
.	.
.	.
.	.
	.
.	.
	.
.	.
.	.
.	.

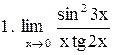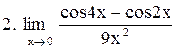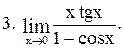
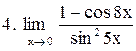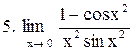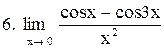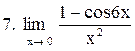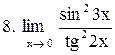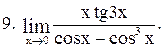
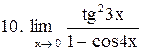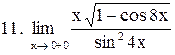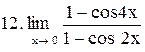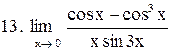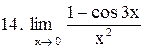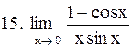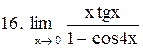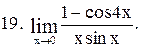
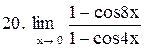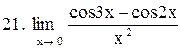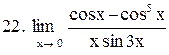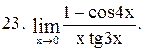
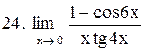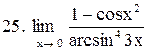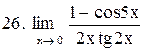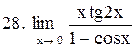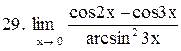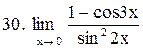З а д а ч а 19

Пример 21

Вычислить предел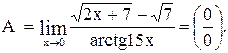

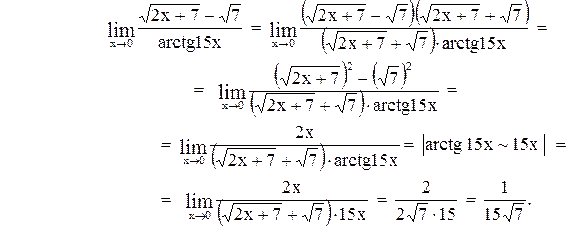
Контрольные варианты к задаче 19

Вычислить пределы функций:

	.
.	.
	.
.
	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
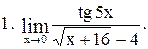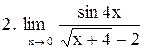
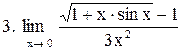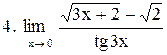
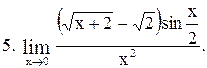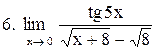
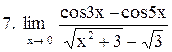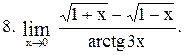
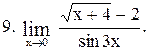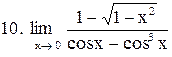
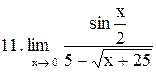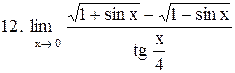
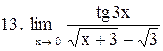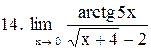
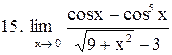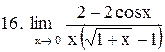
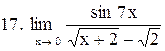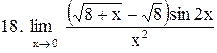
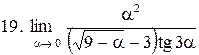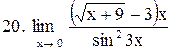
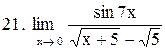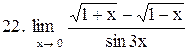
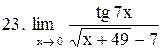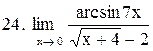
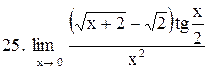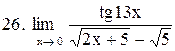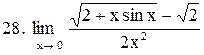
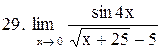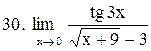