
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример 28
|
|
Исследовать функцию на непрерывность. Установить характер разрыва. Построить график функции
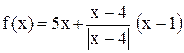 .
.
так как 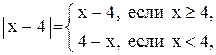
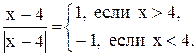
Функция 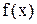 не определена в точке
не определена в точке 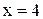 . Эта функция может быть записана в виде
. Эта функция может быть записана в виде
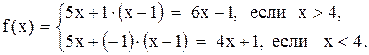
Каждое из аналитических выражений непрерывно, следовательно, функция 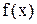 имеет разрыв только в точке
имеет разрыв только в точке  , где она не определена. Слева от этой точки
, где она не определена. Слева от этой точки
функция задана формулой 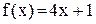 . Следовательно,
. Следовательно, 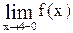 =
=
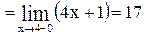 . Справа от точки
. Справа от точки 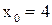 функция задана формулой
функция задана формулой 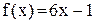 , поэтому
, поэтому 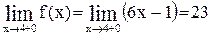 . Односторонние пределы в точке
. Односторонние пределы в точке  конечны, но не равны между собой. Предел функции в точке
конечны, но не равны между собой. Предел функции в точке  не существует. Функция имеет разрыв в этой точке, который является неустранимым разрывом I рода (скачком).
не существует. Функция имеет разрыв в этой точке, который является неустранимым разрывом I рода (скачком).
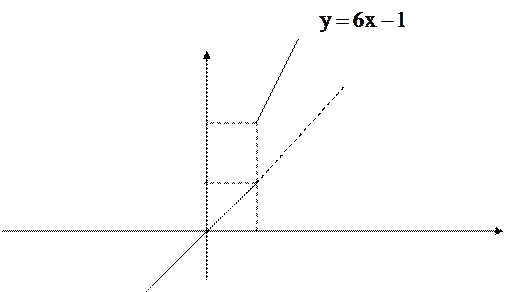
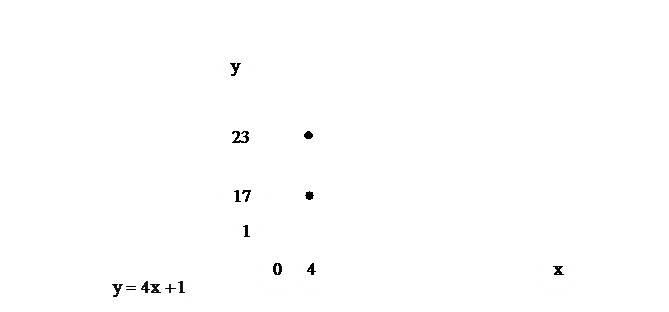
Контрольные варианты задачи 26
Исследовать функцию на непрерывность. В точках разрыва установить характер разрыва. Схематично построить график функции:
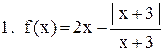 . .
| 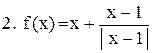 . .
|
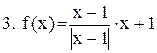 . .
| 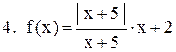 . .
|
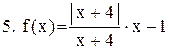 . .
| 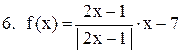 . .
|
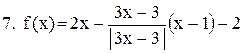 . .
| 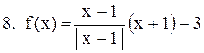 . .
|
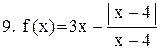 . .
| 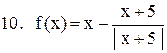 . .
|
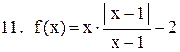
| 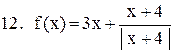 . .
|
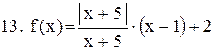 . .
| 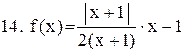 . .
|
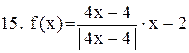 . .
| 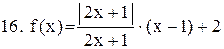 . .
|
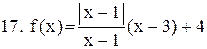 . .
| 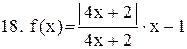 . .
|
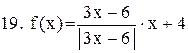 . .
| 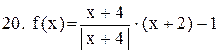 . .
|
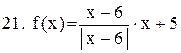 . .
| 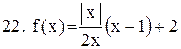 . .
|
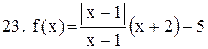 . .
| 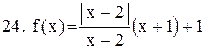 . .
|
 . .
| 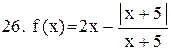 . .
|
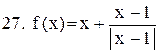 . .
| 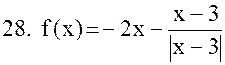 . .
|
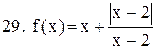 . .
| 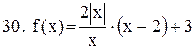
|