
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Момент количества движения системы материальных точек
|
|
Суммарный момент количества движения (момент импульса) системы частиц относительно произвольно выбранной точки (оси) в инерциальной системе отсчета будет равен
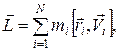 (2.7.1)
(2.7.1)
где 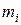 — масса
— масса 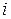 — той точки,
— той точки, 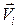 — ее скорость в системе XOYZ. Положение точек системы показано на рис. 3.1.10.
— ее скорость в системе XOYZ. Положение точек системы показано на рис. 3.1.10.
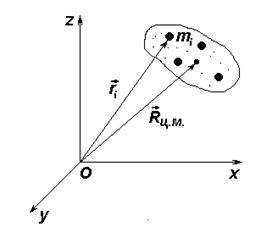
Рис. 2.6. К определению момента количества движения
системы материальных точек
Если вектор 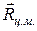 представляет собой вектор, характеризующий положение центра масс относительно начала отсчета, то это выражение можно записать в более удобном виде:
представляет собой вектор, характеризующий положение центра масс относительно начала отсчета, то это выражение можно записать в более удобном виде:
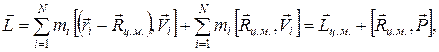
где 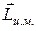 — момент импульса относительно центра масс и
— момент импульса относительно центра масс и 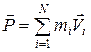 —полный импульс (или количество движения) частиц. Слагаемое
—полный импульс (или количество движения) частиц. Слагаемое 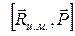 представляет момент импульса центра масс относительно начала отсчета и зависит от выбора системы отсчета. Слагаемое
представляет момент импульса центра масс относительно начала отсчета и зависит от выбора системы отсчета. Слагаемое 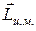 не зависит от выбора начала отсчета.
не зависит от выбора начала отсчета.
Между частицами действуют внутренние силы. Примем без доказательства утверждение, что их суммарный момент равен нулю. Тогда уравнение изменения момента импульса принимает следующий вид:
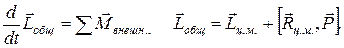 (2.7.2)
(2.7.2)
Во многих случаях за начало отсчета удобно выбирать центр масс.
В такой системе отсчета точки осуществляют вращение вокруг оси, проходящей через этот центр. В свою очередь, центр масс движется под действием результирующей силы. Вращение точек системы определяется результирующим моментом внешних сил.
Твердое тело, как мы уже отмечали, можно рассматривать как совокупность малых элементов с массой 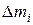 . Поэтому полученные результаты применимы и к рассмотрению вращательного движения твердого тела. Чтобы прояснить основную физическую идею этой главы и выявить основные трудности, рассмотрим следующие примеры.
. Поэтому полученные результаты применимы и к рассмотрению вращательного движения твердого тела. Чтобы прояснить основную физическую идею этой главы и выявить основные трудности, рассмотрим следующие примеры.
Пример. Пусть имеется тонкий обруч радиусом R, например, велосипедное колесо. Приведем этот обруч во вращательное движение относительно оси проходящей через центр обруча и перпендикулярной его плоскости (рис. 2.7).
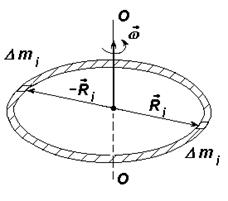
Рис. 2.7. Вращающийся обруч
В этом случае массы всех элементов находятся на одинаковом расстоянии от оси. Поэтому модуль момента импульса обруча равен
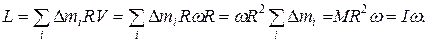
Здесь мы использовали тот факт, что все точки обруча движутся с одинаковыми по модулю скоростями, равными 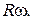
По аналогии с вращением материальной точки величину 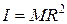 назовем моментом инерции обруча относительно оси, проходящей через центр масс и перпендикулярной плоскости обруча.
назовем моментом инерции обруча относительно оси, проходящей через центр масс и перпендикулярной плоскости обруча.
Докажем, что в данном примере имеет место следующее соотно-
шение:
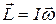 .
.
Вернемся к основному определению момента импульса, и поместим начало отсчета в центр масс тела. Тогда имеем:
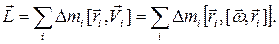
Раскрывая двойное векторное произведение, получим:
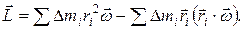 (2.7.3)
(2.7.3)
Направление векторов 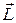 и
и 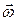 совпадают только в том случае, если второе слагаемое (2.7.3) равно нулю. Это возможно при выполнении одного из двух условий. Во-первых, если векторы
совпадают только в том случае, если второе слагаемое (2.7.3) равно нулю. Это возможно при выполнении одного из двух условий. Во-первых, если векторы 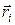 и
и 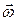 взаимно перпендикулярны, и, следовательно, скалярное произведение
взаимно перпендикулярны, и, следовательно, скалярное произведение 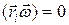 . В рассматриваемом примере это условие выполнено. Во-вторых, если тело является однородным и симметричным относительно оси вращения. В этом случае каждому элементу
. В рассматриваемом примере это условие выполнено. Во-вторых, если тело является однородным и симметричным относительно оси вращения. В этом случае каждому элементу 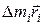 найдется соответствующий элемент
найдется соответствующий элемент 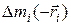 и при суммировании второе слагаемое (2.7.3) обратиться в нуль. В случае
и при суммировании второе слагаемое (2.7.3) обратиться в нуль. В случае
с обручем и это условие оказывается выполненным.
Следовательно, при выполнении одного из двух найденных условий уравнение вращательного движения твердого тела имеет следующий вид:
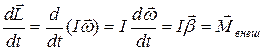 . (2.7.4)
. (2.7.4)
Если отмеченные условия не выполняются, то описание вращательного движения становится сложным.
Для тела произвольной формы с произвольным распределением масс момент импульса 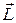 уже не равен простому произведению скалярной величины на вектор
уже не равен простому произведению скалярной величины на вектор 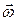 . Именно это обстоятельство и является причиной сложного поведения вращающихся тел. Уравнение вращательного движения и в этом случае имеет вид:
. Именно это обстоятельство и является причиной сложного поведения вращающихся тел. Уравнение вращательного движения и в этом случае имеет вид:
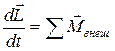 . (2.7.5)
. (2.7.5)