Теорема Штейнера

Предположим, что мы умеем вычислять моменты инерции относительно любой оси, проходящей через центр масс. Теперь возникает задача вычисления момента инерции тела относительно произвольной оси. Она решается с помощью теоремы Штейнера.

Эта теорема утверждает, что момент инерции тела относительно любой оси вращения равен моменту инерции относительно параллельной ей оси, проходящей через центр масс, сложенному с произведением массы тела на квадрат расстояния центра масс тела от оси вращения.

Для доказательства теоремы рассмотрим некую ось С, проходящую через центр масс и параллельную ей ось О, отстоящую от оси С на расстоянии а. Ось О может находиться и вне тела. Обе оси перпендикулярны плоскости чертежа (рис. 2.12).

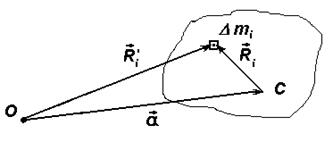
Рис. 2.12. К доказательству теоремы Штейнера

Из рис. 2.12 видно, что положение элемента массы 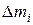относительно этих осей определяется векторам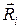и и 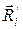, связь между которыми имеет вид:

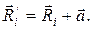
Квадрат расстояния 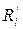равен скалярному произведению

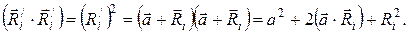
Тогда момент инерции тела относительно оси О можно представить в следующем виде:

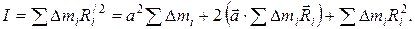
Последнее слагаемое в этом выражении есть момент инерции тела относительно оси, проходящей через центр масс. Обозначим его через 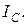Сумма 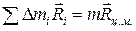. Напомним, что оси О и С параллельны и следовательно, вектор 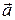перпендикулярен оси С. Поэтому скалярное произведение 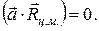Таким образом, мы получаем:

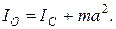(2.10.1)

\ 2.11. Уравнение движения твердого тела.

Абсолютно твердое тело имеет шесть степеней свободы и, следовательно, его движение описывается с помощью шести дифференциальных уравнений второго порядка. Три из них описывают движение центра масс твердого тела:

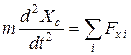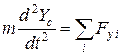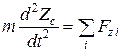, , , (2.11.1)

где 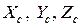— координаты центра масс тела, 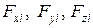— проекции внешних сил на оси координат, m — масса тела. Три других являются уравнениями моментов относительно осей ОХ, ОУ и ОZ в декартовой системе координат:

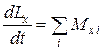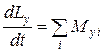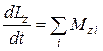, , , (2.11.2)

где L _x, L _y, L _z — моменты импульса системы относительно осей ОХ, ОУ, ОZ, а M _x, M _y, M _z — моменты внешних сил относительно этих же осей.

Если перемещать точку приложения силы вдоль линии ее действия, то моменты сил и результирующие силы не будут меняться, если мы имеем дело с абсолютно твердым телом. В этом случае не будут меняться и уравнения движения (2.11.1), (2.11.2).

Если найдены решения уравнений (2.11.1), (2.11.2), при известных начальных условиях, то определены и шесть координат, характеризующих движение твердого тела. Эти координаты являются функциями времени. Однако системы уравнений (2.11.1) и (2.11.2) не всегда позволяют получить решение в аналитической форме. В этом случае говорят, что уравнение движения не удается проинтегрировать, и решение уравнений находят путем численного интегрирования.