
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Примеры ЗЛО
|
|
Лабораторная №1
Метод линейной оптимизации
В этой лабораторной работе будут рассмотрены теория и примеры использования количественных методов и моделей, цель которых – найти оптимальную стратегию управления в условиях, когда все параметры и правила управления системой чѐ тко определены и не подвержены никаким случайным воздействиям. В таких задачах используется метод линейной оптимизации, цель которого – составление оптимальных планов производства, продаж, закупок, перевозок, оптимальное финансовое планирование, оптимальная организация рекламных кампаний и др. Планирование – одна из основных функций менеджмента.
Примеры ЗЛО
1). Оптимальный производственный план. Пусть предприятие может производить несколько видов продукции А1, А2, …, Аn. Для производства каждого вида из них, требуется разное количество одних и тех же ресурсов B1, B2, …, Bn (материалы, электроэнергия, рабочая сила и т. д.). Продажа одного изделия каждого типа приносит определенную прибыль с1, с2, …, сn. Так как из имеющихся на предприятии ресурсов можно ежедневно производить различное количество изделий, то и прибыль будет неодинаковой. Отсюда, может существовать множество различных производственных планов, каждому из которых соответствует определенное значение прибыли P и определенный расход каждого ресурса, который в свою очередь может быть ограниченным. В задаче требуется найти такой вариант производственного плана, при котором прибыль была бы максимальной.
2). Организация транспортных перевозок. Пусть имеется сеть оптовых баз А1, А2, …, Аm, с которых однотипная продукция может доставляться потребителям в магазины B1, B2, …, Bn. Продукцию можно привезти с любой базы Ai в любой магазин Bj. Стоимость перевозки единицы груза разная, она известна и для любой пары Ai→ Bj равна cij. Ясно, что лучше выбирать такие пары (база-магазин), для которых эта стоимость наименьшая. Запасы продукции на базах, а также потребности магазинов ограничены. В задаче требуется составить план перевозок {Хij}, чтобы суммарные транспортные расходы P были наименьшими, а также удовлетворены все требования потребителей, а груз, имеющийся на базах, весь вывезен.
3). Выбор инвестиционных проектов. Инвестиционный отдел банка рассматривает множество возможных проектов вложения денег на следующий год J1, J2, …, Jn. Каждый проект в конце года должен принести определенную прибыль P1, P2, …, Pn. Для каждого проекта определен количественный индекс надежности r1, r2, …, rn. Каждый проект Jiв течение года требует определенное ежемесячное финансирование а, а, …, а. Банк рассчитывает, что его денежные поступления в следующем году составят S1, S2, …, S12д.ед. Какие проекты выбрать, а какие отвергнуть, чтобы планируемого притока наличности хватило для финансирования отобранных проектов?
4). Реклама и маркетинг. Рекламная компания хочет, чтобы еѐ рекламные объявления достигли, по крайней мере, 1 млн. человек. Она планирует провести рекламу через местное TV, радио, почту, газеты и электронную почту. Известна маркетинговая оценка эффективности рекламы в различных каналах, данные о количестве объектов, размещения рекламы, средней аудитории, охватывающей данные СМИ и цены на рекламную акцию. Компанию интересует минимальная стоимость рекламы, а также, сколько денег следует вложить в каждый канал.
Можно привести еще ряд примеров, но все они имеют некоторые общие черты, их можно объединить по составлению математической модели.
Область исследования операций, которая занимается оптимизацией, называется математическим программированием. Теоретической основой линейной оптимизации (ЛО) является линейное программирование, которое является одной из составляющих математического программирования. Модели линейного программирования очень важны, так как много задач в самых разных сферах деятельности, которые могут быть проанализированы с помощью моделей линейного программирования. Существуют эффективные и универсальные алгоритмы решения ЗЛП, реализованные на ЭВМ, а также, методы анализа моделей ЛП позволяют исследовать модель на чувствительность при изменении еѐ параметров.
Постановка ЗЛО
При построении математической модели задачи линейной оптимизации, прежде всего, необходимо определить количественную характеристику цели, которой надо достичь в процессе оптимизации, - целевую функцию. Это может быть максимальная прибыль или минимальные издержки (в денежном, временном или в каком-либо другом выражении). Целевая функция показывает, почему одно рассматриваемое решение лучше или хуже другого.
Целевая функция зависит от величин, называемых переменными решения (неизвестными), которые можно изменять, разыскивая оптимальное решение.
Цель оптимизации – найти такие значения переменных решения, при которых целевая функция достигает максимума или минимума. Любая оптимизация всегда проводится при наличии некоторых ограничений – условий, ограничивающих изменение переменных решения. Эти ограничения могут диктоваться:
а) вторичными целями (например, рассматривая задачу о минимизации рисков инвестиционного портфеля, мы, одновременно, хотим добиться ожидаемой прибыли);
б) ограниченностью ресурсов, находящихся в распоряжении (денежных, временных, материальных и др.);
в) установленными “правилами игры” (рыночные ограничения, нормативные акты, любые требования субъекта, принимающего решения и т.д.)
Любой набор переменных решения, удовлетворяющих ограничениям, называют допустимым решением (или допустимым планом). Таких планов может быть множество. Допустимое решение, которое отвечает наибольшему или наименьшему значению целевой функции, называется оптимальным решением. Обычно это решение одно, но встречаются модели, когда одному оптимальному плану соответствует множество допустимых решений.
Линейная оптимизация имеет дело с моделями, в которых целевая функция линейно зависит от переменных решения, ограничения также представляют собой линейные уравнения или неравенства. В линейных моделях, кроме неизвестных, присутствуют постоянные числа, их называют параметрами. Параметры модели (например, тарифы перевозок) определяют вид и значение целевой функции, оптимальное решение также зависит от параметров модели, т.е. если их изменить, изменится и оптимальное решение. Это очень важно, потому что, изменяя параметры, можно что-то менять в управляемой системе. Но в ходе поиска оптимального решения параметры считают неизменными. После его определения, параметры можно изменить и найти новое оптимальное решение. Методы анализа модели ЛО не только позволяют получить оптимальное решение, но и дают информацию о том, как может изменяться это решение при изменении параметров модели, т.е. есть возможность получить ответы на вопросы типа “что, если”, а это очень важно для лица, принимающего решение.
Для решения задач ЛО можно использовать надстройку к программе электронных таблиц MS Excel, которая называется «Поиск решения».
Как было уже сказано, теоретической основой задач линейной оптимизации, является линейное программирование. Модели линейного программирования очень важны, так как много задач в самых разных сферах деятельности, которые могут быть проанализированы с помощью моделей линейного программирования.
Существуют эффективные и универсальные алгоритмы решения ЗЛП, реализованные на ЭВМ, а также, методы анализа моделей ЛП позволяют исследовать модель на чувствительность при изменении еѐ параметров.
Математическая модель ЗЛО.
Рассмотрим «Линейную модель оптимального планирования».
Мини-кейс: “Оптимальный план производства”.
Задача №1 «Оптимальный план выпуска продукции мебельного цеха»
Цех может выпускать два вида продукции: шкафы и тумбы для телевизора.
На каждый шкаф расходуется 3, 5м стандартных ДСП, 1м листового стекла, и 1 человека-день трудозатрат. На тумбу расходуется 1м ДСП, 2м стекла, и 1 человеко-день трудозатрат. Прибыль от продажи 1 шкафа составляет 200у.е., а 1 тумба – 100у.е. Материальные и трудовые ресурсы ограничены: в цехе работают 150 рабочих, запасы ДСП на день составляют 350м, а стекла – 240м. Какое количество шкафов и тумб должен выпустить цех, чтобы получить максимальную прибыль? Оформим данные задачи в виде таблицы 1.
Таблица 1.
Параметры задачи №1
| Ресурсы | Шкаф | Тумба | Запасы |
| ДСП | 3, 5 | ||
| Стекло | |||
| Труд | |||
| ПРИБЫЛЬ |
Решение.
1) Прежде всего определим цель задачи и вид целевой функции. В данном случае мы хотим максимизировать прибыль, следовательно, целевая функция должна вычислять полную прибыль. В задаче задана прибыль, которую приносит каждый вид произведѐ нной мебели. Поэтому полная прибыль P будет определяться этой прибылью и количеством произведѐ нной мебели каждого вида.
Пусть X и Y – соответственно количество шкафов и тумб, выпускаемых цехом.
Прибыль от продажи одного шкафа равна 200у.е., значит, прибыль от продажи X шкафов будет 200∙ X. Аналогично прибыль от продажи Y тумб равна 100∙ Y. Общая прибыль от продажи шкафов и тумб будет равна P=200X+100Y. Глядя на выражение целевой функции, можно легко увидеть, что, чем больше будут значения X и Y, тем больше будет прибыль P. Но увеличивать беспредельно ежедневный выпуск шкафов и тумб невозможно, так как ресурсы ограничены.
2. На этом этапе надо выяснить, при каких ограничениях надо найти максимальную прибыль. Запишем эти ограничения. Начнем с трудовых ресурсов.
Поскольку каждый рабочий за 1 день может сделать либо 1 шкаф, либо 1 тумбу, ясно, что общее количество выпущенных изделий не должно превышать числа рабочих в цехе. То есть, общий расход труда на X шкафов и Y тумб, будет
1∙ X+1∙ Y≤ 150.
Аналогично записывается неравенство, отражающее ограниченность ежедневных запасов ДСП. Поскольку на 1 шкаф расходуется 3, 5м ДСП, а на тумбу – 1м, то суммарный расход ДСП будет 3, 5∙ X+Y, что не должно превышать ежедневного запаса ДСП в цехе, т.е. 350м. Получим неравенство
3, 5∙ X+Y≤ 350.
Рассуждая точно также относительно третьего ресурса – стекла, получим ограничение 1∙ X+2∙ Y≤ 240. Осталось добавить, что переменные решения не могут быть отрицательными, X≥ 0, Y≥ 0.
Получим математическую модель ЗЛО или ЗЛП.
Найти max P=200∙ X+100∙ Y, при ограничениях:
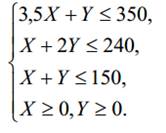
Определение переменных решения, целевой функции и ограничений – это почти все, что должен сделать менеджер, чтобы воспользоваться результатами оптимизации и анализа линейной модели. Дальше необходимо только правильно организовать данные для компьютера на листе MS Excel и запустить задачу на решение.
При организации данных ЗЛП на листе MS-Excel следует отвести отдельные ячейки для параметров, переменных, целевой функции и левых частей ограничений. Ячейки для переменных можно оставить пустыми или ввести в них любые допустимые значения переменных, а в ячейки для целевой функции ограничений ввести формулы, отражающие их функциональную зависимость от переменных и параметров.
Требование линейности означает, что и целевая функция, и ограничения могут представлять собой только суммы произведений коэффициентов на переменные решения. В MS-Excel имеется стандартная математическая функция СУММПРОИЗВ (или SUMPRODUCT), позволяющая быстро вычислять такие суммы произведений. Далее на листе MS-Excel надо сделать все необходимые расчѐ ты для задания ограничений. Когда будем иметь всю информацию, необходимую надстройке “Поиск решения”, приступаем к решению.