Программирования

Хотя сам оптимальный план очень полезен, часто бывает интересно знать, как можно изменить те или иные параметры системы (до этого постоянные), чтобы улучшить решение, получить еще большую прибыль или уменьшить издержки. Значение параметров определяет оптимальное значение переменных и целевой функции. С целью улучшения решения многие параметры могут быть изменены. В наших примерах трудно поменять параметры, характеризующие технологический процесс, но изменить количество ресурсов (запасы), а также отпускные цены на товары вполне возможно. Обычно это связывают с привлечением дополнительных финансовых ресурсов, при этом необходимо ответить на ряд вопросов:

- какой ресурс наиболее сильно влияет на изменение прибыли (издержек)?

- как изменится решение и целевая функция при изменении количества того или иного ресурса?

- если какой-либо продукт не входит в оптимальный план, а по каким-то причинам желательно, чтобы он в него входил, то какой параметр, и в каком направлении следует изменить?

- как повлияет на оптимальный план изменение цен на товары, и можно ли бесконтрольно увеличивать цены? и т.д.

Поиск ответов на подобные вопросы и составляет сущность анализа решения. В задачах ЛП существенную информацию о влиянии изменений параметров можно получить из “отчета об устойчивости” в ходе поиска решения в MS-Excel. Для ответа на другие вопросы типа “что, если” необходимо дополнительное исследование. Некоторое представление о том, как может меняться решение ЗЛП при изменении параметров, можно получить из анализа графического решения задачи.

В процессе поиска оптимального решения MS-Excel формирует отчет об устойчивости, в котором выдает интервал изменений коэффициентов целевой функции, внутри которого их изменения не приводит к изменению оптимального решения. Для получения этого отчета надо: найти оптимальное решение с помощью “Поиска решения”;

- в окне ”Результаты поиска решения” нажать кнопку ”Отчет об устойчивости” (табл. 4);

- в первой таблице отчета об устойчивости “Изменяемые ячейки” есть столбцы “Целевой коэффициент”, “Допустимое увеличение” и “Допустимое уменьшение”. В первом из них даны исходные значения целевых коэффициентов.

Второй и третий столбцы содержат информацию об интервале устойчивости найденного оптимального решения;

- во второй таблице отчета об устойчивости “Ограничения” аналогичные интервалы устойчивости установлены для запасов ресурсов, смысл которых несколько иной. Чтобы его понять, рассмотрим двойственную задачу к задаче №1.

Таблица 4.

Отчѐ т об устойчивости MS Excel для задачи №1

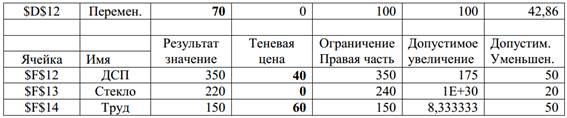
Дальнейшее исследование задачи ЛП связано с изменением запасов ресурсов, для этого необходимо знать их теневые цены. На эти вопросы даѐ т ответ теория двойственности ЗЛП.

Согласно теоремам ЛП, можно предложить, казалось бы, простой метод решения задачи: просто “перебрать” все угловые точки допустимых планов, в каждой из них вычислить значение целевой функции и выбрать ту угловую точку, где целевая функция оптимальна. Однако количество угловых точек области может быть большим и с ростом числа переменных неограниченно увеличиваться.

Однако компьютер, используя надстройку “ Поиск решения” MS-Excel, решит такую задачу очень быстро, используя эффективные методы решения. Этот метод называется “симплекс-метод”. Он не перебирает все угловые точки допустимого множества, а, начав с любой из них, выбирает каждую последующую так, чтобы значение целевой функции в ней было ближе к оптимальному решению. Поэтому симплекс-метод называют методом последовательного улучшения плана.

Симплекс-метод реализуется в три этапа:

1. Нахождение первоначального базисного плана. Для этого определяют линейно - независимые столбцы матрицы, составленной из технологических параметров системы ограничений.

2. Нахождение допустимого базисного решения. С геометрической точки зрения, допустимое решение - это попадание в одну из вершин области допустимых планов, в этом случае все базисные переменные неотрицательные.

3. Нахождение оптимального базисного решения. Найденный допустимый базис проверяют на оптимальность. Для этого подключают целевую функцию и проверяют на ней критерии оптимальности.