Приёмы решения задач ЛП с помощью MS-Excel

Рассмотрим более сложные примеры задач ЛП, с большим количеством переменных решения, которые позволят продемонстрировать дополнительные технические приемы, полезные при исследовании моделей линейного программирования.

Мини-кейс «Планы закупок»

Задача №3 «На кондитерской фабрике».

Небольшая кондитерская фабрика должна закрыться на реконструкцию. Необходимо реализовать оставшиеся запасы сырья для производства конфет из ассортимента фабрики, получив максимальную прибыль. Запасы и расход каждого вида сырья для производства единицы продукции каждого вида, а также получаемая при этом прибыль представлены в таблице 1.6. Мастер цеха, используя свой большой опыт, предлагает выпустить по 200 пакетов каждого вида конфет из ассортимента, утверждая, что ресурсов должно хватить, а прибыль получится 1080у.е. Молодой менеджер, только что окончивший экономический институт, утверждает, что такие проблемы не решаются на глазок, а с помощью линейного программирования.

Хозяин фабрики обещает менеджеру всю прибыль сверх 1080у.е., если он предложит лучший план, чем многоопытный мастер. Все параметры занесѐ м в таблицу 8.

Таблица 8.

Основные параметры задачи «На кондитерской фабрике»

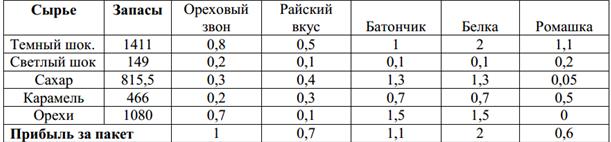
Математическая модель задачи №3. За переменные решения примем количество пакетов каждого из 5 видов конфет, выпускаемых фабрикой.

Обозначим их как X_i, i=1, 2, 3, 4, 5. Тогда целевая функция, прибыль от производства данного количества пакетов каждого вида продукции, будет равна

P=1∙ X₁+0, 7∙ X₂+1, 1∙ X₃+2∙ X₄+0, 6∙ X₅.

Ограничения на переменные: расход каждого вида сырья (в кг) на производство одного пакета каждого продукта можно найти на пересечении строки (сырье) и столбца (продукта) в таблице параметров. Это так называемые технологические коэффициенты производства.

Расход темного шоколада на X₁ пакетов каждого их продуктов не должен превышать запаса этого ресурса. Т.е. ограничение на темный шоколад будет иметь вид:

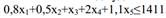
Аналогично можно получить ограничения по другим ресурсам, кроме того, из экономического смысла задачи следует, что все X_i≥ 0.

Решение мини-кейса «На кондитерской фабрике» с помощью MS-Excel

Организуем данные на листе MS-Excel так, как это показано в табл.9.

Таблица 9

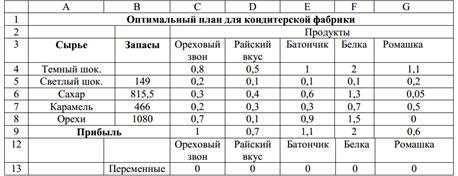
И далее

В ячейках с C13 по G13 содержатся переменные решения. В ячейки B16 по B20 введены формулы, отражающие расход ресурсов на единицу каждого продукта. Повторив алгоритм решения задачи с помощью MS Excel, получим решение. После команды «Выполнить» в ячейках с C13 по G13 (табл.10) можно прочесть ответ. Поскольку количество произведенных пакетов должны быть целыми числами, надо округлить значения полученных переменных до целых так, чтобы ограничения на ресурсы были строго соблюдены. В ячейках с C13 по G13 содержатся значения расходов ресурсов, которые необходимы для получения оптимального плана.

Таблица 10.

Результаты решения задачи «На кондитерской фабрике»

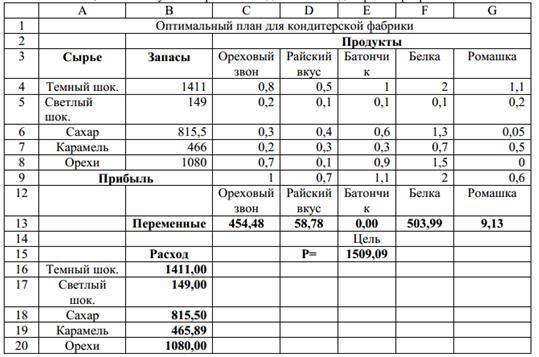
После решения задачи об оптимальном плане для кондитерской фабрики молодой менеджер испытал двойственное чувство. С одной стороны, прибыль, соответствующая найденному им производственному плану, почти на 430 у.е. больше, чем по плану мастера, т.е. он заработал более 400 у.е., с другой стороны, в оптимальный план не вошѐ л его любимый “Батончик”. Как исправить ситуацию. Менеджеру необходимо ответить на следующие вопросы:

1. Как надо изменить норму прибыли для “Батончика”, чтобы он вошѐ л в оптимальный план?

2. Если ввести это изменение в данные и решить задачу заново, как изменится оптимальный план?

3. Какой ресурс является наиболее дефицитным (т.е. максимально влияет на прибыль)?

4. Можно ли сказать (не решая задачу снова), как изменится прибыль от производства, если количество этого ресурса оценено: а) с избытком в 10 весовых единиц; б) с недостатком в 5 единиц?

5. Есть ли другой способ добиться производства “Батончика” кроме изменения нормы прибыли?

Для того, чтобы ответить на эти вопросы, необходимо получить отчѐ т об устойчивости MS-Excel (табл. 11).

Таблица 11.

Отчет об устойчивости MS Excel задачи «На кондитерской фабрике»

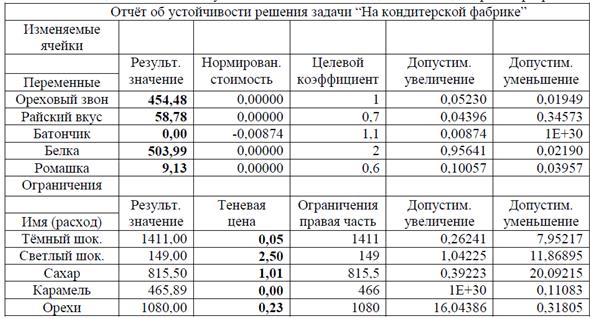
Ответ на вопросы 1 и 2. Согласно отчѐ ту об устойчивости (табл. 10), нормированная стоимость конфеты “Батончик”, не вошедшей в оптимальный план, составляет 0, 00874у.е. Абсолютная величина этого числа показывает, на сколько надо увеличить прибыль от одного пакета этих конфет, чтобы “Батончик” вошѐ л в оптимальный план. Для этого решим задачу ещѐ раз, изменив один параметр, а именно, увеличив цену “Батончика” на 0, 01у.е. В этом случае прибыль станет равной 1, 11у.е. (табл. 12).

Таблица 1.12. Оптимальный план задачи “На кондитерской фабрике”

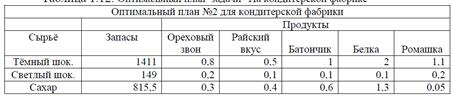
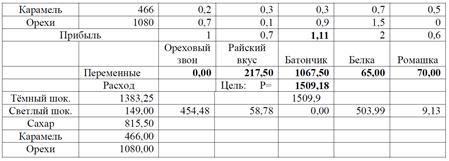
Видим, что малые изменения параметров приводят к серьёзным изменениям решения. Для сравнения, ниже прибыли, записаны результаты с прежней ценой на “Батончик”. В этом случае говорят, что решение задачи неустойчиво. Решение называется неустойчивым, если малые изменения параметров приводят к огромным изменениям решения. Эта неустойчивость особенно опасна при рассмотрении методов выбора решения в условиях риска. В нашей задаче прибыль в обоих случаях почти одинаковая, т.е. неустойчивость решения не страшная. Если ввести целочисленные ограничения на количество пакетов каждого вида продуктов, или потребовать ограничение: количество пакетов “Батончика” было не менее 100, 200, 300, получим альтернативные решения, сильно различающиеся по значениям переменных, но очень близких по прибыли. Это хорошо, т.к. наличие многих “хороших” альтернативных решений позволяет менеджеру выбрать такое, которое в наилучшей степени отвечает тем или иным условиям, которые всегда присутствуют при принятии решений.

Ответ на вопросы 3 и 4. Для ответа на эти вопросы посмотрим отчёт об устойчивости (табл.11). Согласно ему, наибольшей теневой ценой обладает ресурс - “светлый шоколад”. Но интервал устойчивости, соответствующий этой цене, очень маленький (149-11, 87; 149+1, 04). Если запас этого ресурса уменьшить на 10 ед., то реальная прибыль будет ниже:

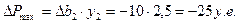
Эту формулу можно использовать, так как Δ b2=-10 попадает в интервал устойчивости. Если запас данного ресурса увеличить на 5 ед., предсказать увеличение прибыли нельзя, т.к. Δ b2=5 выходит за рамки интервала устойчивости. В этом случае задачу надо решать заново.

Ответ на вопрос 5. Необходимо обратить внимание на то, что какой-либо из ресурсов для производства “Батончика” является дефицитным и востребован другим продуктом. “Батончик” конкурирует с “Белкой” за ресурсы: сахар и орехи. Расход этих ресурсов на эти два продукта наибольший. Увеличение запасов этих ресурсов может привести к вхождению “Батончика” в оптимальный план. Так, если увеличить запасы сахара на 40 ед. и заново решить задачу на максимум, получим новый оптимальный план, где “Батончика” будет произведено более 1080 пакетов, прибыль при этом будет P=1547, 8 у.е. 23

В окне ” Добавление ограничения ” существует возможность потребовать целочисленности переменных решения. Для этого надо из предлагаемых ограничений выбрать ограничение “ цел ”. Решение ЗЦЛП в Excel делает невозможным получение информации об устойчивости решения и о теневых ценах. Поэтому “Поиск решения” MS Excel не формирует отчёта об устойчивости, если хотя бы для одной переменной введено условие целочисленности. Рассмотрим задачу.