Основные теоремы двойственности

Теорема 1. Если одна из взаимно двойственных задач имеет оптимальное решение, то его имеет и другая, причем оптимальные значения их линейных функций равны:

Fmax=Сmin

Если линейная функция одной из задач не ограничена, то условия другой задачи противоречивы.

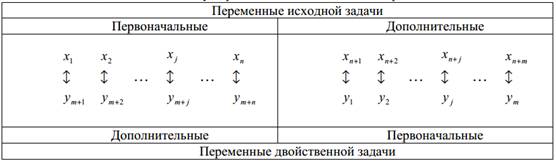
Теорема 2. Первоначальным переменным оптимального решения одной из взаимно двойственных задач соответствуют дополнительные переменныеоптимального решения другой задачи (табл. 6).

Таблица 6.

Связь между переменными двойственной пары задач ЛП

Теорема 3. Переменные оптимального решения двойственной задачи равны абсолютным значениям коэффициентов при соответствующих переменных линейной функции исходной задачи, выраженной через свободные переменные еѐ оптимального решения.

Двойственная задача для задачи ”об оптимальном плане выпуска продукции мебельного цеха”

Задача №1.2.

Пусть имеется покупатель на все ресурсы, используемые для выпуска продукции мебельного цеха (ДСП, стекло и труд). Таблица параметров та же, что и для исходной задачи (табл. 1). Какие цены на эти ресурсы надо назначить, чтобы продать их было выгоднее, чем производить продукцию? Какую минимальную сумму можно выручить от продажи ресурсов при этом условии?

Математическая модель задачи. Так как в задаче три вида ресурсов, то переменных решения тоже будет три. Это цены на ресурсы, которые назначает производитель при продаже: 1м ДСП стоит Y1у.е., 1м стекла – Y2 у.е., 1 день труда рабочего – Y3у.е. Эти цены называют “объективно обусловленными оценками” или “теневыми ценами” (скрытыми доходами). Теневые цены характеризуют ценность ресурсов для производителя.

Целевая функция – это прибыль, которую получит продавец ресурсов, если продаст по этим ценам все имеющиеся ресурсы, т.е.:

C(Y) = 350y₁ + 240y₂ + 150y₃

Однако интерес покупателя в том, чтобы купить эти ресурсы как можно дешевле, т.е. целевую функцию можно рассматривать как издержки покупателя ресурсов, которые необходимо минимизировать, приняв во внимание интересы производителя – продавца ресурсов.

Цель производителя (продавца ресурсов) найти минимальное значение суммарной выручки от продажи всех ресурсов при условии, что продать их было бы не менее выгодно, чем производить из них продукцию.

При записи ограничений производитель использует тот же принцип: если он хочет продать 3, 5 м ДСП, 1 м стекла и 1 день труда рабочего, то он должен получить не меньше, чем прибыль от производства одного шкафа:

3, 5y₁ + y₂ + y₃ ≥ 200,

аналогично для тумбы:

y₁ + 2y₂ + y₃ ≥ 100, где y₁, y₂, y₃ ≥ 0

Итак, получили задачу:

Найти

min C(Y) = 350y₁ + 240y₂ + 150y₃

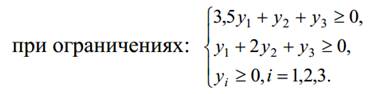
Для проверки теорем теории двойственности можно решить двойственную задачу с помощью MS-Excel.

Получим

min С(Y)=23000 у.е.,

цены на ресурсы: y₁=40; y₂=0; y₃=60.

Бросается в глаза нулевая цена второго ресурса – стекла. Это нулевое значение теневой цены стекла обусловлено тем обстоятельством, что при оптимальном плане выпуска продукции мебельного цеха (зад. №1) ежедневные запасы стекла избыточны, каждый день из 240 м стекла производитель использует только 220 м. Отсюда вывод: “теневые цены” в конкретной производственной ситуации характеризуют ценность ресурса для производителя”. Рассматривая решения двойственной пары задач №1 и №2, можно проследить следующую экономическую связь между ними.

Ясно, что если запасы ресурса избыточны (т.е. не полностью используются в оптимальном плане производства), то теневая цена такого ресурса не приведѐ т к увеличению прибыли, а только увеличит неиспользованный остаток. Теневые цены ресурсов будут изменяться, если изменение их запасов выйдут за пределы интервала устойчивости. Так, если уменьшить ежедневный запас стекла до величины, меньшей, чем 220м, прибыль изменится, теневая цена стекла y2 перестанет быть равной нулю. В таблице 4, в отчѐ те об устойчивости приведены теневые цены и интервалы устойчивости изменения запасов каждого из ресурсов, в котором значения теневых цен сохраняется. Такая информация помогает менеджеру, не решая задачу заново, оценить, запасы, какого ресурса нужно увеличивать, чтобы максимально увеличить прибыль, и каково будет это увеличение. Влияние изменения запаса ресурсов можно прокомментировать следующим образом:

1. При решении симплекс-методом исходной задачи сразу же решается и двойственная задача. Отчѐ т Excel об устойчивости включает таблицу “Ограничения” и в ней колонку “Теневая цена”. Теневые цены – это оценки Y_i двойственной задачи. Они показывают, как меняется целевая функция при малом изменении b_i: ∆ P=Y_i∙ ∆ b_i

2. Эти оценки верны только в пределах устойчивости решения, т.е. пока изменение b_i не изменяет угловую точку области допустимых решений, в которой достигается максимум целевой функции. При этом численные значения переменных решения X_j, конечно, изменяются. При выходе b_i за пределы устойчивости все теневые цены изменятся.

3. Пределы изменения правых частей системы ограничений (b_i), в которых оптимальное решение соответствует той же самой угловой точке, тоже даны в таблице “Ограничения”. Это столбцы - “Допустимое увеличение” и “Допустимое уменьшение” (табл. 4). Причем, если ресурс используется полностью (дефицитный), то существует как верхний, так и нижний пределы. Если же ресурс используется не полностью, верхний предел устойчивости равен бесконечности (10³⁰).

4. Пределы устойчивости для изменения b_i даются при условии, что все остальные значения b_k (k≠ i) остаются неизменными, иначе будут меняться теневые цены.

5. Для оценки влияния одновременного изменения нескольких значений b_i следует вычислить относительные изменения для каждой правой части системы ограничений 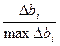, где max ∆ b_i – это предел либо увеличения, либо уменьшения b_i (в зависимости от знака ∆ b_i), и вычислить сумму этих относительных изменений. Если эта сумма больше 1, теневые цены изменятся, если – меньше 1, то не изменятся.

Рассмотрим на нашей задаче “Об оптимальном плане мебельного цеха” как повлияет изменение запасов некоторых ресурсов. Ответим на следующий вопрос:

Как изменится целевая функция (прибыль) при изменении запасов ресурса bi? Все вычисления внесѐ м в табл. 7.

Таблица 7.

Расчет прибыли при изменении запасов ресурсов

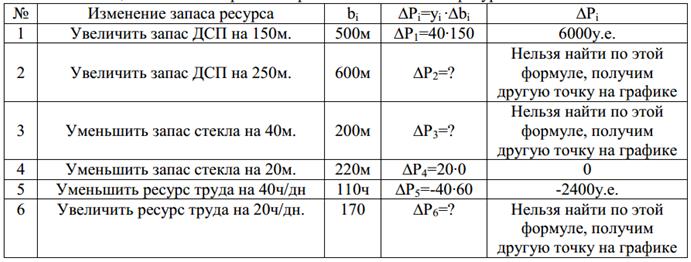
Эти расчеты получены согласно интервалам устойчивости по ресурсам (табл.4), а именно: ДСП(350-50; 350+175), стекло(240-20; ∞), труд(150-50; 150+8, 333).