Задание 1. Вычислите вероятности указанных событий, используя теоремы сложения и умножения вероятностей.

В магазине имеется 10 телевизоров, из которых три имеют дефекты. Посетитель купит телевизор, если для выбора телевизора без дефекта понадобится не более трех попыток. Какова вероятность того, что посетитель купит телевизор.

Задание 2. Вычислите вероятности указанных событий используя формулу полной вероятности и формулу Байеса.

Среди клиентов страховой компании 50% относится к классу малого риска, 30%- к классу среднего риска и 20%- к классу большого риска. Вероятность необходимости выплачивать страховое вознаграждение для класса малого риска равна 0, 01, среднего- 0, 03, большого- 0, 08. Какова вероятность того, что наудачу взятый а) застрахованный клиент получит денежное вознаграждение за период страхования; б) получивший денежное вознаграждение клиент относится к группе малого риска.

Задание3. Вычислите вероятности указанных событий, используя формулу Бернулли

Контрольное задание состоит из 5 вопросов, на каждый из которых дается 4 варианта ответа, причем один из них правильный, а остальные неправильные. Найдите вероятность того что учащийся не знающий ни одного вопроса, дает: а) 3 правильных ответа; б) не менее 3-х правильных ответов (предполагается, что учащийся выбирает ответы наудачу).

Задание4. Составить закон распределения дискретной случайной величины Х, построить многоугольник распределения. Найти F(x) и построить ее график. Найти МХ, ДХ, sХ. Найти Р(Х< x₀), P(x₁ ).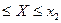

Случайная величина Х- число правильных счетов, если аудиторской проверке подверглись 5 случайно отобранных счетов. Известно, что обычно при таких проверках 3% счетов содержат ошибки

х₀=1 х₁=3 х₂=5

Задание5. Случайная величина Х задана функцией распределения F(x):

а) Является ли случайная величина Х непрерывной?

б) Имеет ли случайная величина Х плотность вероятности f(x). Если имеет, то найдите ее.

В) Постройте схематически графики F(x) и f(x).

г) Найдите МХ, ДХ, sХ

д) Найдите Р(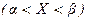

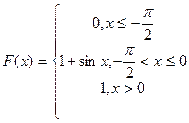
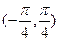
Задание6. Автобусы идут строго по расписанию с интервалом 5 минут. Предполагая что время Х ожидания автобуса на остановке имеет равномерное распределение, найдите: а) плотность вероятности; б) функцию распределения cлучайной величины Х; в) вероятность того что время ожидания не превзойдет 2 мин; г) постройте графики плотности вероятности и функции распределения; д) числовые характеристики данной случайной величины.

Тер.вер-ти

Вариант4.

Задание 1. Вычислите вероятности указанных событий, используя теоремы сложения и умножения вероятностей

В аудиторской фирме работают 7 аудиторов, из которых 3-высокой квалификации, и 5-программистов, из которых 2- высокой квалификации. В командировку надо отправить группу из 3 аудиторов и 2 программистов. Какова вероятность того, что в этой группе окажется по крайне мере 1 аудитор высокой квалификации и хотя бы 1 программист высокой квалификации, если каждый специалист имеет равные возможности поехать в командировку.

Задание 2. Вычислите вероятности указанных событий используя формулу полной вероятности и формулу Байеса.

Если экономика страны будет на подъеме, то вероятность роста стоимости акций некоторой компании оценивается в 0, 75. Если экономика страны не будет успешно развиваться, то эта вероятность будет равна 0, 30. По мнению экспертов вероятность экономического подъема в новом году равна 0, 80. Оцените вероятность того, что акции компании поднимутся в цене в новом году. По прошествии года оказалось, что прогноз относительно роста стоимости акций оказался верным. Найдите вероятность того, что рост стоимости акций сопровождался экономическим ростом в стране.

Задание3. Вычислите вероятности указанных событий, используя формулу Бернулли

Вероятность того что покупателю потребуется обувь 41 размера равна 0, 2. Найдите вероятность того, что из 5 первых покупателей обувь этого размера понадобится: а) одному; б) по крайней мере одному покупателю.

Задание4. Составить закон распределения дискретной случайной величины Х, построить многоугольник распределения. Найти F(x) и построить ее график. Найти МХ, ДХ, sХ. Найти Р(Х< x₀), P(x₁ ).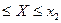

Случайная величина Х- число рентабельных предприятий, попавших в число приватизируемых. В городе 10 машиностроительных предприятий, из которых 6 рентабильных и 4 убыточных. Программой приватизации намечено приватизировать 5 предприятий, случайно отобранных.

х₀=4 х₁=3 х₂=5.

Задание5. Случайная величина Х задана функцией распределения F(x):

а) Является ли случайная величина Х непрерывной?

б) Имеет ли случайная величина Х плотность вероятности f(x). Если имеет, то найдите ее.

В) Постройте схематически графики F(x) и f(x).

г) Найдите МХ, ДХ, sХ

д) Найдите Р(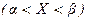

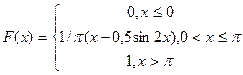, 0< x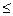

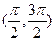
Задание6. Автомат изготавливает детали. Случайные отклонения фактического размера от проектного подчинены нормальному закону со средним квадратическим отклонением s=5мм и математическим ожиданием а=0. Найдите: а) плотность распределения f(x); б) ее график; в) процент годных деталей, изготавливаемых автоматом, при условии, что деталь считается годной, если отклонение не превышает 10 мм; г) в каких границах практически находятся отклонения в размере изготовленных деталей (практически достоверное событие имеет вероятность не меньше 0, 9974)

Тер.вер-ти

Вариант5.

Задание 1. Вычислите вероятности указанных событий, используя теоремы сложения и умножения вероятностей

На полке стоят 10 книг, среди которых 3 книги по теории вероятностей. Наудачу берутся 3 книги. Какова вероятность того, что среди отобранных: а) хотя бы одна книга по теории вероятностей; б) одна книга по теории вероятностей.

Задание 2. Вычислите вероятности указанных событий используя формулу полной вероятности и формулу Байеса.

Директор компании имеет 2 списка с фамилиями претендентов на работу. В 1-м списке-фамилии 6 женщин и 3 мужчин. Во 2-м списке оказалось 4 женщины и 7 мужчин. Фамилия одного из претендентов случайно переносится из 1-го списка во 2-й. Затем фамилия одного из претендентов случайно выбирается из 2-го списка. Найти вероятность того, что выбрана фамилия мужчины. Если предположить, что эта фамилия принадлежит мужчине, чему равна вероятность того, что из 1-го списка была перенесена фамилия женщины.

Задание3. Вычислите вероятности указанных событий, используя формулу Бернулли

На автобазе имеется 6 автомашин. Вероятность выхода на линию каждой из них равна 0, 8. Найдите: а) вероятность нормальной работы автобазы, если для этого необходимо иметь на линии не меньше 5автомашин; б) вероятности на линию выйдет 3 автомашины.

Задание4. Составить закон распределения дискретной случайной величины Х, построить многоугольник распределения. Найти F(x) и построить ее график. Найти МХ, ДХ, sХ. Найти Р(Х< x₀), P(x₁ ).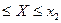

Случайная величина Х- число промахов. С вероятностью попадания при одном выстреле 0, 7 охотник стреляет по дичи до первого попадания, но успевает сделать не более трех выстрелов.

х₀=1 х₁=0 х₂=2

Задание5. Случайная величина Х задана функцией распределения F(x):

а) Является ли случайная величина Х непрерывной?

б) Имеет ли случайная величина Х плотность вероятности f(x). Если имеет, то найдите ее.

В) Постройте схематически графики F(x) и f(x).

г) Найдите МХ, ДХ, sХ

д) Найдите Р(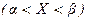

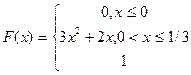(0, 1)

Задание6. Известно, что время Т- промежуток времени между двумя последовательными событиями простейшего потока событий имеет показательный закон распределения с параметром l, где l- интенсивность потока. Поступающие на АТС вызовы образуют простейший поток событий. Среднее число вызовов, поступающих за 1 минуту, равно 2. Т- время между двумя последовательными вызовами. Найдите: а) f(t)- плотность распределения случайной величины Т; б) F(t)- функцию распределения; в) графики f(t) и F(t); г) числовые характеристики Т (МХ, ДХ, sХ); д) вероятность того, что за 3 минуты поступит 2 вызова.

Тер.вер-ти

Вариант6.

Задание 1. Вычислите вероятности указанных событий, используя теоремы сложения и умножения вероятностей

Вероятность своевременного выполнения студентом контрольной работы по каждой из трех дисциплин равна соответственно 0, 6; 0, 5; 0, 8.Найти вероятность своевременного выполнения контрольной работы студентов: а) по двум дисциплинам; б) хотя бы по двум дисциплинам; в) хотя бы по одной дисциплине.

Задание 2. Вычислите вероятности указанных событий используя формулу полной вероятности и формулу Байеса.

Экспертно-импортная фирма собирается заключить контракт на поставку сельскохозяйственного оборудования в одну из развивающихся стран. Если основной конкурент фирмы не станет одновременно претендовать на заключение контракта, то вероятность получения контракта оценивается в 0, 45; в противном случае- в 0, 25. По оценкам экспертов компании вероятность того, что конкурент выдвинет свои предложения по заключению контракта, равна 0, 40. Чему равна вероятность заключения контракта? Контракт все же заключен, какова вероятность того, что конкурент выдвигал свои предложения?

Задание3. Вычислите вероятности указанных событий, используя формулу Бернулли

В среднем по 15% договоров страховая компания выплачивает страховую сумму. Найти вероятность того, что из десяти договоров с наступлением страхового случая будет связано с выплатой страховой суммы: а) три договора; б) менее двух договоров.

Задание4. Составить закон распределения дискретной случайной величины Х, построить многоугольник распределения. Найти F(x) и построить ее график. Найти МХ, ДХ, sХ. Найти Р(Х< x₀), P(x₁ 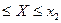). Случайная величина Х- число проданных автомобилей черного цвета. В магазине имеется 12 автомобилей и среди них 7- черного цвета, 5- белого цвета. Представители фирмы обратились в магазин с предложением о продаже им 4 автомобилей. Учесть, что автомобили отбирались случайным образом. х₀=4 х₁=0 х₂=3

Задание5. Непрерывная случайная величина Х задана дифференциальной функцией распределения. Найдите: а) значение параметра а, при котором f(x) будет плотностью распределения случайной величины Х; б) интегральную функцию распределения F(x), постройте графики F(x) и f(x); в) числовые характеристики; г) Найдите Р(.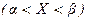

1.

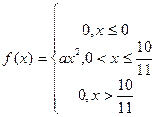
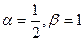
Задание6. Завод изготовляет шарики для подшипников. Номинальный диаметр шариков d₀=5мм. Вследствие неточности изготовления шарика фактический его диаметр- случайная величина Х, распределенная по нормальному закону со средним значением d₀ и средним квадратическим отклонением s_d=0, 05 мм. При контроле бракуются все шарики, диаметр которых отличается от номинального больше чем на 0, 1 мм. Найдите: а) плотность вероятности случайной величины Х; б) построить график f(x); в) средний процент шариков которые отбраковываются; г) интервал, в котором практически находится диаметр изготовляемых шариков.