Тер.вер-ти

Вариант7.

Задание 1. Вычислите вероятности указанных событий, используя теоремы сложения и умножения вероятностей

Вероятность для компании, занимающейся строительством терминалов для аэропортов, получить контракт в стране А равна 0, 4; вероятность выиграть его в стране В равна 0, 3. Вероятность того, что контракты будут заключены и в стране А и в стране В, равна 0, 12. Чему равна вероятность того, что: а) компания получит контракт хотя бы в одной стране; б) не получит ни одного контракта; в) получит контракт только в одной стране.

Задание 2. Вычислите вероятности указанных событий используя формулу полной вероятности и формулу Байеса.

На химическом заводе установлена система аварийной сигнализации. Когда возникает аварийная ситуация, звуковой сигнал срабатывает с вероятностью 0, 95. Звуковой сигнал может сработать случайно и без аварийной ситуации с вероятностью 0, 02. Реальная вероятность аварийной ситуации равна 0, 004. Какова вероятность того, что звуковой сигнал сработает. Предположим, что звуковой сигнал сработал. Чему равна вероятность реальной аварийной ситуации.

Задание3. Вычислите вероятности указанных событий, используя формулу Бернулли

Вероятность того, что стрелок хотя бы раз попадет в мишень при четырех выстрелах равна 0, 9984. Найти: а) вероятность попадания при одном выстреле, если эта вероятность постоянна и не зависит от результатов предыдущих выстрелов; б) вероятность одного попадания при трех выстрелах.

Задание4. Составить закон распределения дискретной случайной величины Х, построить многоугольник распределения. Найти F(x) и построить ее график. Найти МХ, ДХ, sХ. Найти Р(Х< x₀), P(x₁ ).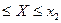

Случайная величина Х- число правильных ответов студента на вопросы теста. Экзаменационный тест содержит 4 вопроса, каждый из которых имеет 5 возможных ответов и только один их них верный.

х₀=2 х₁=3 х₂=4

Задание5. Непрерывная случайная величина Х задана дифференциальной функцией распределения. Найдите: а) значение параметра а, при котором f(x) будет плотностью распределения случайной величины Х; б) интегральную функцию распределения F(x), постройте графики F(x) и f(x); в) числовые характеристики; г) Найдите Р(.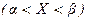

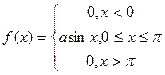
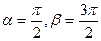
Задание6. На перекрестке стоит автоматический светофор, в котором 1 минуту горит зеленый свет и 0, 5 минуты- красный, затем опять 1 минуту горит зеленый свет, 0, 5 минут- красный и т.д. Некто подъезжает к перекрестку на машине в случайный момент, не связанный с работой светофора. Найдите: а) плотность распределения его времени ожидания у светофора; б) функцию распределения случайной величины времени ожидания; в) построить графики данных функций; г) вероятность того что он проедет перекресток не останавливаясь; д) числовые характеристики данной случайной величины.

Тер.вер-ти

Вариант8.

Задание 1. Вычислите вероятности указанных событий, используя теоремы сложения и умножения вероятностей

Экспедиция издательства отправила газеты в 3 почтовых отделения. Вероятность своевременной доставки газет в первое отделение равна 0, 9 во второе-0, 9, в третье-0, 8. Найти вероятности событий: а) только одно отделение получит газеты вовремя; б) хотя бы одно отделение получит газеты вовремя.

Задание 2. Вычислите вероятности указанных событий используя формулу полной вероятности и формулу Байеса.

При слиянии акционерного капитала 2-х фирм аналитики фирмы, получающей контрольный пакет акций, полагают, что сделка принесет успех с вероятностью, равной 0, 65, если председатель совета директоров поглощаемой фирмы выйдет в отставку; если он откажется, то вероятность успеха будет равна 0, 30. Предполагается, что вероятность ухода в отставку председателя составляет 0, 70. Чему равна вероятность успеха сделки? Допустим, что сделка принесла успех, чему равна вероятность того, что отставка председателя состоялась?

Задание3. Вычислите вероятности указанных событий, используя формулу Бернулли

Произведено 5независимых испытаний, каждое из которых заключается в одновременном подбрасывании 2 монет. Найдите: а) вероятность того, что ровно в 3 испытаниях появились по 2 герба; б) вероятность того, что 2 герба выпадет не менее трех раз.

Задание4. Составить закон распределения дискретной случайной величины Х, построить многоугольник распределения. Найти F(x) и построить ее график. Найти МХ, ДХ, sХ. Найти Р(Х< x₀), P(x₁ ).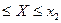

Случайная величина Х- число станков, которые в течение часа не потребуют внимания рабочего. Рабочий обслуживает 3 независимо работающих станка. Вероятность того, что в течение часа станок не потребует внимания рабочего, равна для первого станка 0, 7, для второго-0, 75, для третьего-0, 9.

х₀=2 х₁=0 х₂=2

Задание5. Непрерывная случайная величина Х задана дифференциальной функцией распределения. Найдите: а) значение параметра а, при котором f(x) будет плотностью распределения случайной величины Х; б) интегральную функцию распределения F(x), постройте графики F(x) и f(x); в) числовые характеристики; г) Найдите Р(.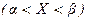

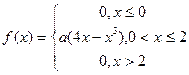
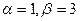
Задание6. Случайная величина Х- прогноз, являющийся средним результатом индивидуальных прогнозов большого числа аналитиков. Пусть этот прогноз относительно величины банковской процентной ставки в текущем году подчиняется нормальному закону со средним значением а=9% и стандартным отклонением s=2, 6%. Из группы аналитиков случайным образом отбирается один человек. Найдите: а) f(x); б) F(x); в) вероятность того, что согласно прогнозу этого аналитика уровень процентной ставки: 1) превышает 11%; 2) окажется менее 14%; г) в каком интервале практически можно ожидать величину процентной ставки.

Теория вер-ти

Вариант9.

Задание 1. Вычислите вероятности указанных событий, используя теоремы сложения и умножения вероятностей

Мастер обслуживает 4 станка, работающих независимо друг от друга. Вероятность того, что первый станок в течение смены потребует внимания рабочего, равна 0, 3, второй-0, 6, третий-0, 4 и четвертый-0, 25. Найти вероятность того, что в течение смены хотя бы один станок не потребует внимания и вероятность того, что один станок потребует внимания мастера.

Задание 2. Вычислите вероятности указанных событий используя формулу полной вероятности и формулу Байеса.

Вероятность того, что клиент банка не вернет заем в период экономического роста, равна 0, 04, а в период экономического кризиса- 0, 13. Предположим, что вероятность того, что начнется период экономического роста, равна 0, 65. Чему равна вероятность того, что случайно выбранный клиент банка не вернет полученный кредит? Какова вероятность того, что это произойдет в период экономического роста?

Задание3. Вычислите вероятности указанных событий, используя формулу Бернулли

Вероятность хотя бы одного попадания при двух выстрелах для стрелка равна 0, 99. Найти вероятность четырех попаданий при пяти выстрелах, если вероятность попадания при каждом выстреле одна и та же.

Задание4. Составить закон распределения дискретной случайной величины Х, построить многоугольник распределения. Найти F(x) и построить ее график. Найти МХ, ДХ, sХ. Найти Р(Х< x₀), P(x₁ ).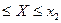

Случайная величина Х- число фальшивых авизо, которые могут быть выявлены в ходе проверки. В банк поступило 30 авизо. Подозревают, что среди них 3 фальшивых. Тщательной проверке подвергается 10 случайно выбранных авизо.

х₀=1 х₁=0 х₂=1

Задание5. Непрерывная случайная величина Х задана дифференциальной функцией распределения. Найдите: а) значение параметра а, при котором f(x) будет плотностью распределения случайной величины Х; б) интегральную функцию распределения F(x), постройте графики F(x) и f(x); в) числовые характеристики; г) Найдите Р(.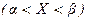

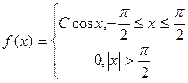
Задание6. На числовой оси оt задан простейший поток событий. Случайная величина Т- время между двумя последовательными событиями потока. В среднем в минуту поступает 4 заявки. Т- имеет показательный закон распределения с параметром l. Найдите: а) плотность распределения f(t) случайной величины Т; б) функцию распределения F(t); в) постройте графики f(t), F(t); г) числовые характеристики Т; д) вероятность того, что в течение 5 мин поступит хотя бы одна заявка.

Теория вер-ти

Вариант 10.

Задание 1. Вычислите вероятности указанных событий, используя теоремы сложения и умножения вероятностей

Охотник выстрелил три раза по удаляющейся цели. Вероятность попадания в нее в начале стрельбы равна 0, 8, а после каждого выстрела уменьшается на 0, 1. Найдите вероятность того, что он: а) промахнется все три раза; б) попадет хотя бы один раз; в) попадет два раза.

Задание 2. Вычислите вероятности указанных событий используя формулу полной вероятности и формулу Байеса.

Транснациональная компания обсуждает возможность инвестиций в некоторое государство с неустойчивой политической ситуацией. Менеджеры оценивают вероятность успеха (в терминах годового дохода от субсидий в течение 1-го года работы) в 0, 55, если политическая ситуация будет благоприятной; в 0, 30, если политическая ситуация будет нейтральной; в 0, 10, если политическая ситуация в течение года будет неблагоприятной. Менеджеры компании также полагают, что вероятности благоприятной, нейтральной и неблагоприятной политических ситуаций соответственно равны: 0, 60; 0, 20; 0, 20. Чему равна вероятность успеха инвестиций? Чему равна вероятность, что успех инвестиций произойдет в неблагоприятной политической обстановке в стране?

Задание3. Вычислите вероятности указанных событий, используя формулу Бернулли

В урне 9 белых и один черный шар. Какова вероятность того, что при 10 извлечениях с возвращением каждого шара будет извлечен хотя бы раз черный шар. Сколько раз нужно производить извлечения, чтобы вероятность получить хотя бы раз черный шар была не меньше 0, 9.

Задание4. Составить закон распределения дискретной случайной величины Х, построить многоугольник распределения. Найти F(x) и построить ее график. Найти МХ, ДХ, sХ. Найти Р(Х< x₀), P(x₁ ).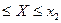

Случайная величина Х- число проверенных стандартных деталей. Вероятность изготовления нестандартной детали 0, 1. Из партии контролер берет деталь и проверяет ее на стандартность. Если деталь оказывается нестандартной, то дальнейшие испытания прекращаются, а вся партия задерживается. Если же деталь окажется стандартной, то контролер берет следующую и т.д., но всего он проверяет не более 4 деталей.

х₀=4 х₁=0 х₂=2

Задание5. Непрерывная случайная величина Х задана дифференциальной функцией распределения. Найдите: а) значение параметра а, при котором f(x) будет плотностью распределения случайной величины Х; б) интегральную функцию распределения F(x), постройте графики F(x) и f(x); в) числовые характеристики; г) Найдите Р(.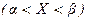

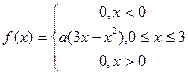
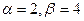
Задание6. Предположим, что в течение года цена на акции некоторой компании есть случайная величина, распределенная по нормальному закону с математическим ожиданием, равным 48 у.е., и стандартным отклонением, равным 6. Найдите: а) f(x); б)F(x); в) вероятность того что в случайно выбранный день обсуждаемого периода цена за акцию была:

1) более 60 у.е.; 2) между 40 и 50 у.е. за акцию;

г) интервал, в котором практически может находится цена акции.