
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Уравнения вида .
|
|
Это уравнение имеет решение только при условии 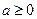 .
.
По определению модуля данное уравнение распадается на совокупность двух уравнений:
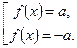
Примеры.
1.1. Решить уравнение:  .
.
Решение: По определению модуля получаем совокупность двух линейных уравнений:
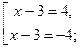
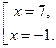
Ответ: 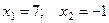 .
.
1.2. Решить уравнение: 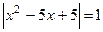 .
.
Решение: По определению модуля уравнение распадается на совокупность двух уравнений:
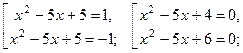
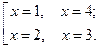
Ответ: 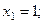
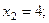
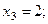
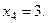
2. Уравнения вида 
По определению модуля данное уравнение распадается на совокупность двух смешанных систем:
1) 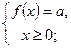 2)
2) 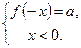
Так как функция 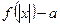 четная, то ее корни будут существовать парами противоположных чисел, т.е. если
четная, то ее корни будут существовать парами противоположных чисел, т.е. если 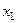 – корень данного уравнения, то и
– корень данного уравнения, то и 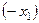 также корень данного уравнения. Следовательно, достаточно решить одну из двух смешанных систем, добавив в ответ к полученным корням им противоположные значения.
также корень данного уравнения. Следовательно, достаточно решить одну из двух смешанных систем, добавив в ответ к полученным корням им противоположные значения.
Примеры.
2.1. Решить уравнение: 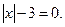
Решение: Рассмотрим систему:

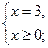
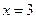 .
.
Следовательно, корнями данного уравнения являются числа 3 и –3.
Ответ: 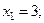
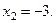
2.2. Решить уравнение: 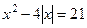 .
.
Решение: Рассмотрим систему:
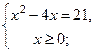
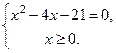
Корнями уравнения 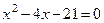 являются числа
являются числа 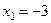 и
и 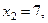 из которых условию
из которых условию 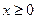 удовлетворяет
удовлетворяет 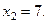
Следовательно, корнями данного уравнения являются числа 7 и –7.
Ответ: 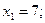
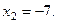
3. Уравнения вида 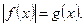
Данное уравнение по определению модуля распадается на совокупность двух смешанных систем:
1) 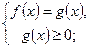 2)
2) 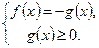
Примеры.
3.1. Решить уравнение: 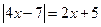
Решение: По определению модуля данное уравнение равносильно совокупности следующих смешанных систем:
1) 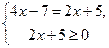
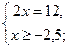

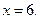
| 2) 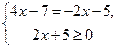

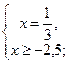
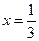
|
Ответ: 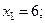
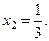
3.2. Решить уравнение: 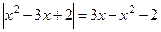
Решение: Решить следует две смешанные системы:
1) 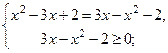
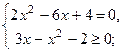
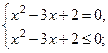
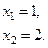
| 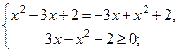
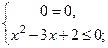
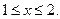
|
Ответ: 
4. Уравнения вида 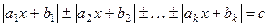
Такие уравнения решаются по следующему плану:
1) Находят значения 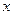 , при переходе через которые меняется знак выражений
, при переходе через которые меняется знак выражений 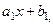
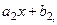
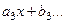
 т.е.
т.е. 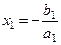 ,
, 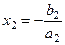 ,
, 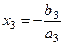 ,...,
,..., 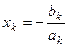 .
.
2) Отмечают найденные значения 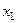 ,
,  ,...,
,..., 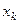 на числовой прямой, пусть для определенности
на числовой прямой, пусть для определенности 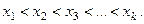
3) Рассматривают данное уравнение последовательно на промежутках: 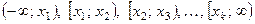 .
.
На каждом промежутке получается некоторое линейное уравнение, которое решают и в ответ отбирают те значения корней, которые содержатся в соответствующих промежутках.
Примеры
4.1. Решить уравнение: 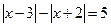 .
.
Решение:
1) 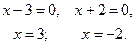
 |
2)
3) a) 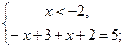
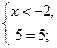
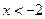 .
.
b) 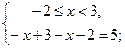
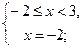
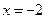
с) 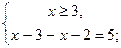
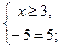 корней нет.
корней нет.
Ответ: 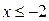
4.2. Решить уравнение: 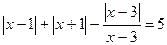
Решение:
1) 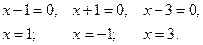
2)
 |
3) а) 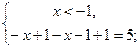
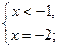
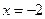 .
.
б) 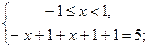
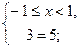 корней нет.
корней нет.
в) 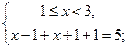
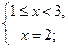
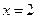 .
.
г) 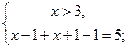
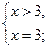 корней нет.
корней нет.
Ответ: 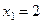
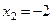
Примечание. Аналогично решаются и уравнения, содержащие под знаком модуля нелинейные зависимости.
5. Уравнения вида 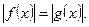
В соответствии с определением модуля данное уравнение равносильно совокупности двух уравнений:
1) 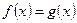 2)
2) 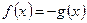
Можно, используя свойство модуля 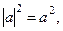 заменить решение данного уравнения решением уравнения
заменить решение данного уравнения решением уравнения 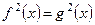 .
.
Примеры.
5.1. Решить уравнение 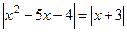 .
.
Решение: Заменим данное уравнение совокупностью двух уравнений:
1) 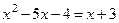 ; 2)
; 2) 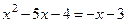 ;
;
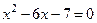 ;
; 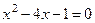 ;
;
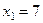 ,
, 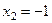 ;
; 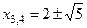 .
.
Ответ: 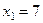 ,
, 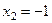 ,
, 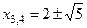 .
.
5.2. Решить уравнение 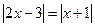 .
.
Решение: Используя свойство модуля числа, заменим данное уравнение уравнением
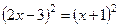 ;
;
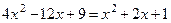 ,
,
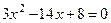 ,
,
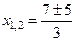 ,
,
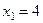 ,
, 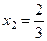 .
.
Ответ: 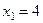 ,
, 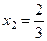 .
.