
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Неравенства вида .
|
|
Это неравенство имеет решение только при условии 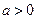 .
.
Используя определение понятия модуля заменим данное неравенство равносильной ему системе неравенств:
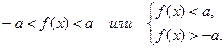
Примеры.
1.1 Решить неравенство 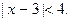
Решение.
По определению модуля получаем систему неравенств: 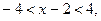 откуда следует, что
откуда следует, что 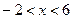 .
.
Ответ: (-2; 6).
1.2. Решить неравенство.
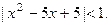
Решение
По определению модуля неравенство равносильно системе неравенств:
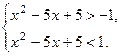
Решив каждое неравенство системы, получаем:
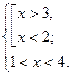
 |
Воспользовавшись геометрической интерпретацией решений неравенств, выберем решение системы:
Ответ: (1; 2) È (3; 4).
2. Неравенства вида 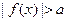
Это неравенство при 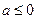 выполняется во всей области определения функции
выполняется во всей области определения функции 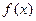 .
.
Если 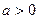 , то по определению модуля данное неравенство равносильно совокупности двух неравенств:
, то по определению модуля данное неравенство равносильно совокупности двух неравенств:
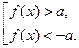
Примеры.
2.1. Решить неравенство 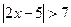 .
.
Решение.
По определению модуля данное неравенство равносильно совокупности двух неравенств:
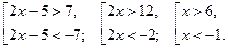
Ответ: (-¥; -1); (6; ¥).
2.2. Решить неравенство 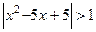 .
.
Решение.
По определению модуля неравенство равносильно совокупности двух неравенств:
1) 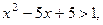
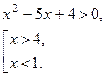
| 2) 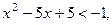
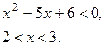
|
Ответ: 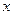 < 1, 2<
< 1, 2< 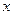 < 3,
< 3, 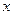 > 4.
> 4.
3. Неравенства вида 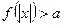 и
и 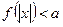
По определению понятия модуля каждое из данных неравенств равносильно совокупности двух систем неравенств:
1) 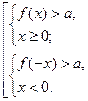 2)
2) 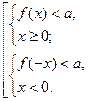
Примеры.
3.1. Решить неравенство 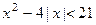
Решение.
По определению модуля данное неравенство равносильно совокупности двух систем неравенств:
А) 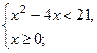
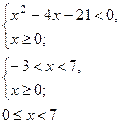
| Б) 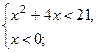
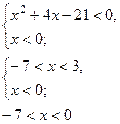
|
Ответ: (-7; 0) È [0; 7).
3.2. Решить неравенство 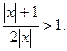
Решение.
Область определения данного неравенства 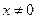 . Т.к. в области определения
. Т.к. в области определения 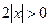 , то данное неравенство равносильно неравенству:
, то данное неравенство равносильно неравенству:
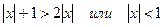 ,
,
используя определение модуля, заменяем данное неравенство совокупностью систем неравенств:
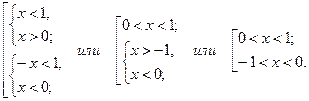
Ответ: (-1; 0) È (0; 1).
Примечание.
Полученное в ходе преобразований 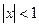 , можно решить как неравенство типа
, можно решить как неравенство типа 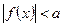 .
.
4. Неравенство вида 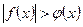
По определению модуля неравенство равносильно совокупности двух систем неравенств:
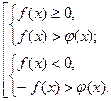
Примеры.
4.1. Решить неравенство 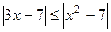 .
.
Решение. Неравенство равносильно совокупности двух систем неравенств:
1) 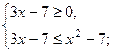 2)
2) 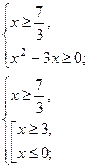
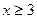
| 3) 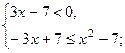 4)
4) 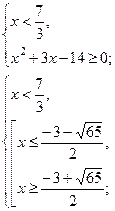
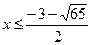
|
Ответ: 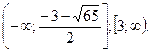
4.2. Решить неравенство: 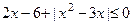 .
.
Решение. Неравенство равносильно совокупности двух систем неравенств:
1) 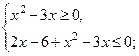
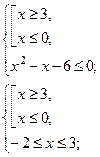
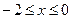 и и 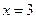
| 2) 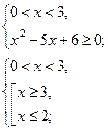
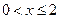
|
Ответ: [-2; 2] È {3}.