Неравенства вида . Такие неравенства решаются по алгоритму, аналогичному алгоритму решению соответствующих уравнений:

Такие неравенства решаются по алгоритму, аналогичному алгоритму решению соответствующих уравнений:

1) Найти значения х, при переходе через которые меняется знак выражений 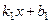, ,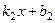..., , 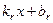т.е. решить совокупность уравнений , ,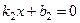..., 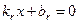и найти корни этих уравнений , ,..., .

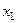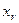2) Отметить найденные значения 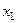, ,..., 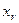на числовой прямой (пусть для определенности < <...< ).

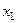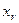3) Рассмотреть данное неравенство последовательно на промежутках 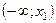; ;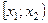...; 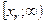, решить полученную совокупность неравенств и в ответ отобрать те промежутки или значения 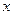, которые содержатся в соответствующих промежутках.

Примечание. Аналогично решаются и неравенства, содержащие под знаком модуля нелинейные зависимости.

Примеры.

5.1. Решить неравенство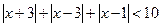

Решение.

1) Найдем значения х, при переходе через которые меняются знаки выражений , , :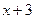

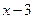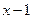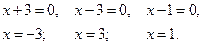
2) Отметим найденные значения 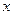на числовой прямой:

3) Рассмотрим данное неравенство на четырех образовавшихся промежутках и отберем соответствующие решения, т.е. решим совокупность четырех систем неравенств:

а)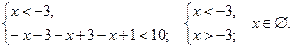

б)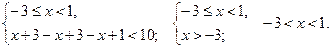

в)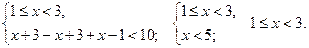

г)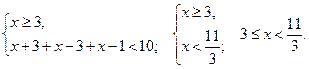

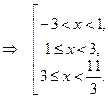
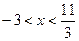. Ответ: