
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задание 1.
|
|
Высшая математика
Функции нескольких переменных
Методические указания
к выполнению типового расчета
Сызрань 2004
Составители: к. ф.-м. н. Анисимов В.Н., Богданова С.М.,
Корпен И.В.
УДК
Высшая математика: Методические указания
Функции нескольких переменных
Самар. Гос. техн. ун-т; Сост. К.ф.-м. н. Анисимов В.Н., Богданова С.М., Корпен И.В.
Сызрань 2004 г.; ________ с.
Методические указания к решению типового расчета по теме «Функции нескольких переменных».
Методические указания предназначены для студентов дневного отделения специальностей 100400; 180400; 210200.
Рецензент
Введение
Требования к выполнению типовых расчетов
1. Задание получает индивидуально каждый студент, согласно своему порядковому номеру в журнале из методического пособия.
2. Типовые задания выполняются в отдельных тетрадях. При решении делать ссылки на используемые теоремы и формулы. В конце решения записывается ответ или делается вывод.
3. Завершающим этапом является защита студентом типового расчета. Во время защиты студент должен правильно отвечать на теоретические вопросы и давать объяснения по решению задач.
Теоретические вопросы
1. Что называется функцией двух (трех) переменных, ее областью определения.
2. Непрерывность функции нескольких переменных в точке; в области.
3. Определение частных производных 1-го порядка. Дифференцирование сложных функций.
4. Определение полного дифференциала функции в данной точке.
5. Определение частных производных высших порядков. Теорема о равенстве смешанных производных функции двух переменных.
6. Производная функции в данном направлении и градиент функции.
7. Определение экстремума функции двух переменных. Необходимые и достаточные условия существования экстремума функции двух переменных.
8. Правило нахождения наибольшего и наименьшего значений функции в замкнутой области.
9. Нахождение условных экстремумов функции двух переменных.
10. Метод наименьших квадратов при нахождении функции на основании экспериментальных данных.
Примеры решения задач.
Задание 1.
Найти область определения функции 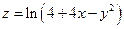 .
.