Задание 2. Доказать, что функция удовлетворяет условию .

Доказать, что функция 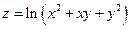удовлетворяет условию .

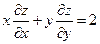Решение.

Находим частные производные:

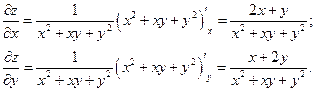
Подставляем 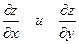в данное уравнение:

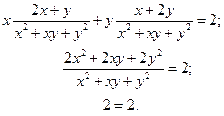
Полученное тождество показывает, что функция действительно удовлетворяет данному уравнению.

Задание 3.

Показать, что выражение 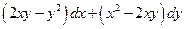(1) есть полный дифференциал некоторой функции 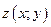и найти эту функцию.

Решение.

Ведем обозначения .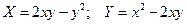

Для того, чтобы выражение (1) было полным дифференциалом функции 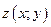необходимо и достаточно выполнение условия: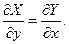

Найдем 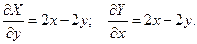Следовательно, выражение (1) есть полный дифференциал. Полный дифференциал выражается формулой: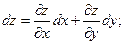

где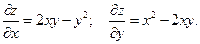

Интегрируя первое равенство по 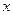, находим искомую функцию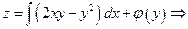

.

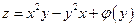Тогда частная производная от z по у:

.

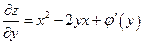Но из условия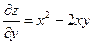

Найдем 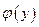из уравнения