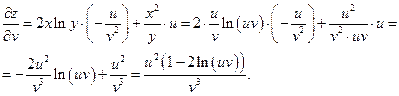Задание 4. Заменив приращение функции дифференциалом, приближенно вычислить .

Заменив приращение функции дифференциалом, приближенно вычислить .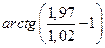

Решение.

Введем в рассмотрение функцию .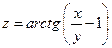

Значение этой функции в точке М(2; 1):

Число 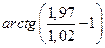есть приращенное значение этой функции в точке М(2; 1), если х получае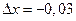т приращение , получает приращение .

Приращенное значение функции в точке равно значению функции в этой точке плюс полное приращение функции, т.е. .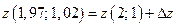

Полное приращение функции приближенно равно полному дифференциалу этой функции в точке: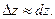

Дифференциал функции

.

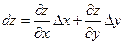Частные производные данной функции:

Значение дифференциала в точке М(2; 1):

.

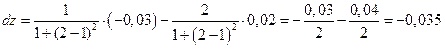
Поэтому .

.

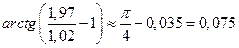Задание 5.

Найти частные производные сложной функции 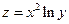, где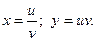

Решение.

Находим сначала частные производные данных функций.

;

.

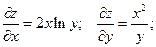
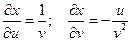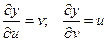Производные сложной функции 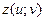вычисляются по формулам: