Критерий (Пирсона) для простой гипотезы

Пусть 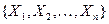выборка из генеральной совокупности 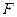. Проверяется гипотеза против альтернативы .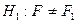

Представим выборку в виде группированного ряда, разбив предполагаемую область значений случайной величины на 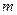интервалов. Пусть 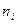- число элементов выборки попавших в 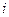-ый интервал, а 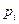- теоретическая вероятность попадания в этот интервал при условии истинности 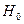. Составим статистику , которая характеризует сумму квадратов отклонения наблюдаемых значений 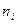от ожидаемых 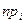по всем интервалам группирования.

Теорема Пирсона. Если 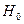верна, то при фиксированном 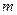и

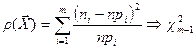. (1)

Таким образом, статистику 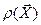можно использовать в качестве статистики критерия согласия для проверки гипотезы о виде закона распределения, который будет иметь вид:

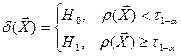, , (2)

где 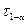-квантиль распределения .

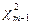Данный критерий называется критерием 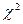или критерием согласия Пирсона.

Замечание. Критерий не состоятелен для альтернатив, для которых 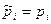для всех 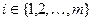. Поэтому, следует стремиться к как можно большему числу интервалов группирования. Однако, с другой стороны, сходимость к 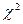величины 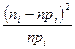обеспечивается ЦПТ, то есть ожидаемое значение 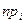для каждой ячейки не должно быть слишком мало. Поэтому обычно число интервалов выбирают таким образом, чтобы .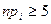