Студопедия

Главная страница Случайная страница

КАТЕГОРИИ:

АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника






Приложение 2. Пример выполнения задания. Дана выборка объемом из неизвестного распределения :


⇐ ПредыдущаяСтр 4 из 4




Дана выборка объемом 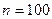из неизвестного распределения :

 

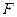4, 81 7, 03 4, 95 0, 25 13, 00 26, 52 1, 40 3, 19 0, 07 1, 99
11, 48 15, 45 5, 17 14, 65 8, 09 0, 38 2, 34 1, 14 0, 39 1, 56
2, 58 17, 15 0, 47 1, 75 13, 74 11, 50 8, 75 1, 08 0, 51 2, 68
0, 53 9, 04 3, 82 1, 01 5, 13 6, 80 4, 52 6, 69 3, 04 9, 41
0, 61 7, 58 4, 26 0, 14 3, 60 1, 27 2, 97 8, 63 3, 46 0, 57
0, 21 20, 35 5, 96 3, 81 3, 35 1, 93 1, 70 0, 71 1, 97 4, 87
21, 17 6, 28 0, 12 6, 02 4, 92 1, 06 2, 94 10, 82 3, 57 8, 04
4, 49 5, 35 1, 07 1, 44 0, 07 1, 61 8, 54 14, 11 9, 63 7, 90
0, 74 2, 96 0, 04 5, 23 16, 01 12, 32 0, 15 1, 36 16, 36 5, 48
9, 88 5, 14 6, 81 1, 27 7, 33 10, 11 1, 88 1, 52 1, 14 5, 62

 

Построим статистический ряд, осуществив группировку данных. Находим 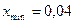, 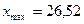. Число интервалов группирования 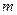определяем по формуле Стерджесса: 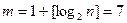. Для удобства возьмем в качестве нижней границы первого интервала значение 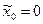, а в качестве верхней границы последнего интервала значение 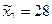, тогда длина каждого интервала группирования будет равна 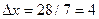. Подсчитывая частоты, получаем следующий ряд:

 

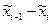
Интервал 0 - 4 4 - 8 8 - 12 12 - 16 16 - 20 20 - 24 24 - 28
Частота              

 

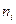
Видим, что частоты распределены по интервалам крайне неравномерно, поэтому делаем перегруппировку данных, добиваясь более равномерного распределения частот по интервалам. В результате получаем следующий ряд:

 

Интервал 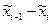0 - 1, 5 1, 5 - 3 3 - 5 5 - 7 7 - 10 10 - 16 16 - 27
Середина 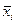0, 75 2, 25     8, 5   21, 5
Частота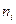              
Относительная частота 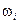0, 28 0, 15 0, 15 0, 13 0, 13 0, 1 0, 06
Плотность частоты 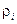0, 1867 0, 1000 0, 0750 0, 0650 0, 0433 0, 0250 0, 0055

 

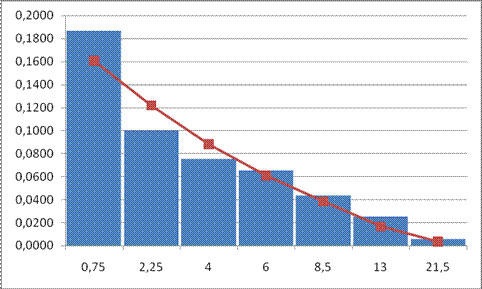
Соответствующая гистограмма приведена на рисунке.

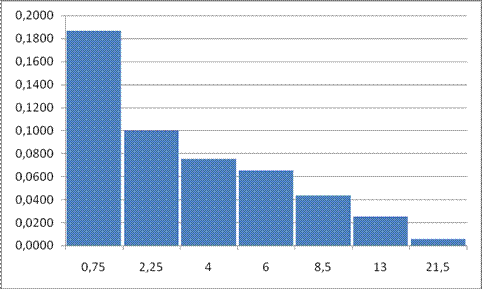
Анализируя гистограмму, видим, что распределение экспериментальных данных похоже на показательное распределение. Таким образом, выдвигаем гипотезу о том, что выборочные данные имеют показательное распределение. В качестве оценки неизвестного параметра 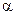, этого распределения возьмем оценку, полученную по методу моментов (через первый момент). Так как 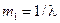, то 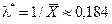. Вычислим значения плотности показательного распределения 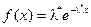в точках, соответствующих серединам интервалов группирования, и сравним гистограмму с графиком плотности:

 

Интервал 0 - 1, 5 1, 5 - 3 3 - 5 5 - 7 7 - 10 10 - 16 16 - 27
Середина 0, 75 2, 25     8, 5   21, 5
Плотность частоты 0, 1867 0, 1000 0, 0750 0, 0650 0, 0433 0, 0250 0, 0055
Теоретическая плотность 0, 1605 0, 1218 0, 0882 0, 0610 0, 0385 0, 0168 0, 0035

 

Найдем также оценки коэффициента асимметрии и эксцесса распределения и сравним их с коэффициентом асимметрии и эксцессом показательного распределения.

Выборочный коэффициент асимметрии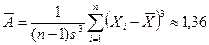

Выборочный эксцесс .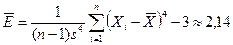

Коэффициент асимметрии для показательного распределения 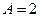, эксцесс 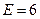. Хотя различие есть, тем не менее можно утверждать, что данные выборочные характеристики имеют смещение (относительно нуля) в сторону характеристик показательного закона.

Примерим критерий Пирсона для проверки нашей гипотезы о законе распределения выборочных данных. Подсчитаем вероятности 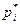попадания в каждый интервал при условии, что генеральная совокупность имеет показательное распределение с параметром 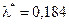: 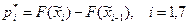, 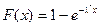- функция распределения показательного закона. Причем для последнего интервала, полагаем 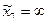и, соответственно, 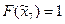, поскольку теоретически для показательного распределения плотность отлична от нуля на интервале 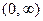. Далее находим ожидаемые значения - 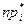и нормированные квадраты отклонений 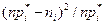по всем интервалам. Результаты оформляем в виде таблицы:

 

Интервал 0 - 1, 5 1, 5 - 3 3 - 5 5 - 7 7 - 10 10 - 16 16 - 27
Частота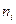              
Вероятность 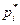0, 242 0, 183 0, 177 0, 123 0, 117 0, 106 0, 052
Ожидаемые значения 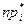24, 16 18, 32 17, 74 12, 27 11, 69 10, 59 5, 24
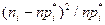
0, 61 0, 60 0, 42 0, 04 0, 15 0, 03 0, 11

 

Находим наблюдаемое значение статистики критерия Пирсона: .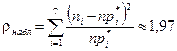

Зададим уровень значимости 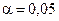. Для заданного уровня значимости и числа степеней свободы 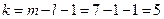( 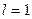- так как один параметр распределения 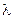мы оценивали по выборке) найдем критическое значение статистики, как критическую точку распределения 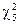уровня 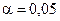(или что тоже самое – квантиль уровня 0, 95): 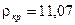. (Критическую точку заданного уровня можно получить, например, используя функцию пакета EXCEL – ХИ2ОБР).

Так как 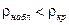, то гипотеза о распределении данных по показательному закону принимается.

Уточним значение 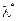, минимизируя наблюдаемое значение статистики 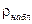. Используя последовательные итерации, можно получить оценку 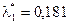, при которой наблюдаемое значение 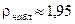. Видим, что в данном случае эта оценка практически не отличается от оценки метода моментов.

Найдем также достигнутый уровень значимости, то есть такое значение 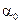, для которого при истинности нашей гипотезы 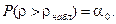Можно воспользоваться, например, функцией пакета EXCEL – ХИ2РАСП. Для 5 степеней свободы и 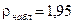получим .

 

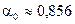Приложение 3. Варианты заданий.

Вариант 1.

-0, 29 2, 64 -0, 76 -3, 58 -0, 31 -0, 53 2, 48 -0, 07 -2, 02 0, 02
-1, 70 -3, 76 -2, 54 -0, 60 -0, 36 3, 21 -2, 37 -0, 54 -0, 98 -0, 31
0, 23 -0, 22 -2, 90 -0, 40 1, 82 1, 01 0, 56 0, 74 -2, 18 3, 78
1, 70 1, 38 -1, 18 0, 12 -0, 07 4, 29 1, 06 -0, 37 -0, 35 -2, 66
1, 56 -1, 36 -0, 87 -0, 36 -0, 17 -0, 71 3, 08 0, 85 -0, 03 -0, 82
0, 88 0, 12 0, 13 -0, 19 -0, 18 -0, 05 -1, 15 3, 69 0, 78 -0, 93
0, 02 0, 10 1, 74 -1, 45 -4, 24 1, 17 -0, 45 -0, 92 -0, 96 0, 74
-0, 52 -0, 58 0, 32 1, 09 -0, 21 -2, 42 -0, 04 -0, 87 0, 60 -0, 55
-0, 84 -3, 65 0, 30 -0, 94 -0, 06 -0, 07 -2, 64 -2, 30 -0, 49 0, 74
-0, 47 -2, 38 -0, 62 -0, 38 0, 61 0, 47 -1, 97 0, 45 0, 33 0, 65

 

Вариант 2.

12, 67 9, 98 9, 46 9, 55 6, 48 4, 49 5, 70 11, 92 14, 24 9, 25
15, 16 7, 15 13, 27 5, 46 7, 20 5, 05 5, 90 16, 16 7, 64 7, 83
2, 69 3, 40 3, 64 11, 34 4, 29 6, 32 4, 43 5, 45 7, 97 8, 03
16, 37 6, 57 5, 96 10, 43 8, 34 14, 19 11, 75 14, 84 4, 75 7, 60
6, 24 7, 98 2, 95 9, 85 5, 57 11, 08 8, 37 9, 55 15, 31 6, 13
10, 17 4, 81 2, 78 9, 20 11, 80 7, 94 6, 15 13, 25 13, 85 7, 19
15, 18 6, 81 7, 99 7, 88 10, 32 11, 12 7, 04 8, 08 4, 86 13, 23
5, 77 14, 04 9, 53 6, 46 3, 70 1, 88 10, 28 3, 15 8, 47 4, 86
5, 66 5, 36 5, 96 12, 86 8, 77 9, 11 8, 71 6, 27 6, 44 3, 49
8, 02 14, 96 9, 46 11, 20 9, 33 11, 39 4, 02 7, 21 4, 75 4, 68

 

Вариант 3.

1, 15 0, 57 3, 90 0, 82 1, 77 0, 78 1, 15 0, 80 0, 33 1, 04
0, 34 0, 50 4, 94 0, 06 3, 76 0, 22 5, 66 0, 13 0, 91 0, 27
0, 55 1, 25 3, 79 0, 28 0, 20 1, 70 0, 77 0, 20 0, 25 3, 81
1, 33 0, 13 1, 45 3, 05 0, 06 0, 09 1, 90 3, 58 2, 48 1, 39
2, 30 0, 02 2, 82 0, 07 0, 32 6, 07 1, 65 1, 59 0, 50 0, 92
1, 30 0, 85 2, 42 0, 46 1, 03 0, 92 0, 94 3, 04 0, 50 2, 52
0, 04 0, 75 3, 27 5, 01 1, 99 1, 44 3, 04 1, 35 0, 56 1, 62
1, 73 1, 44 3, 10 1, 09 3, 41 7, 77 0, 16 2, 98 0, 97 4, 20
0, 45 0, 52 0, 42 0, 81 2, 32 0, 35 1, 91 8, 39 1, 79 3, 59
0, 76 0, 00 0, 63 1, 41 0, 77 4, 67 0, 03 1, 01 0, 52 0, 05

 

Вариант 4.

3, 41 5, 25 8, 66 2, 42 4, 76 1, 60 3, 62 4, 85 3, 30 9, 28
9, 26 4, 92 1, 32 2, 39 4, 70 1, 19 5, 94 4, 35 3, 18 2, 52
5, 71 12, 32 4, 42 2, 46 3, 38 1, 19 5, 28 5, 82 5, 97 6, 76
9, 45 2, 86 2, 73 4, 36 9, 89 6, 80 0, 18 2, 06 1, 23 3, 56
0, 64 4, 25 1, 77 12, 16 0, 14 7, 60 7, 15 4, 57 1, 68 0, 21
2, 05 1, 53 1, 63 1, 88 3, 50 1, 93 4, 19 1, 88 2, 61 3, 49
4, 94 1, 18 5, 12 3, 98 5, 15 0, 53 4, 25 4, 97 6, 24 6, 08
11, 43 4, 48 1, 45 1, 38 0, 81 5, 43 6, 18 7, 89 2, 10 2, 70
4, 79 3, 24 3, 99 9, 62 1, 28 3, 90 4, 13 4, 82 1, 66 7, 84
1, 45 4, 79 3, 98 5, 34 1, 67 5, 56 5, 72 6, 38 3, 91 1, 49

 

 

Вариант 5.

4, 93 2, 12 2, 63 1, 28 2, 61 -46, 88 2, 66 -3, 73 3, 40 4, 38
9, 58 1, 21 0, 69 3, 37 2, 41 2, 47 13, 98 3, 09 2, 63 21, 88
1, 17 9, 04 2, 96 2, 84 14, 75 3, 95 4, 17 2, 40 5, 04 2, 83
0, 74 -1, 39 3, 52 -0, 55 27, 23 2, 68 -8, 21 2, 12 6, 40 1, 99
1, 08 -4, 23 3, 82 2, 59 4, 61 1, 14 2, 09 3, 74 2, 14 3, 54
-92, 24 2, 83 3, 63 40, 08 -6, 88 -7, 57 -57, 09 8, 03 75, 41 1, 97
-0, 68 4, 53 4, 94 0, 19 5, 59 4, 94 2, 47 -7, 34 6, 76 5, 38
2, 08 0, 93 5, 86 3, 91 4, 56 37, 38 3, 70 -1, 46 4, 31 -2, 58
4, 59 2, 60 3, 77 3, 94 3, 33 2, 30 -3, 97 40, 48 14, 45 7, 01
-5, 99 -1, 55 4, 48 3, 18 2, 98 3, 41 -18, 20 2, 34 -0, 28 -0, 66

 

Вариант 6.

-0, 07 4, 78 -16, 43 -1, 45 -3, 14 1, 90 -3, 32 29, 29 -2, 24 0, 12
2, 74 1, 50 -1, 42 7, 62 0, 48 0, 37 -0, 38 -1, 68 -0, 36 -0, 13
-6, 14 1, 50 -5, 23 -0, 26 0, 58 6, 69 -6, 22 0, 58 0, 79 2, 85
5, 55 1, 33 11, 17 -0, 14 -0, 78 -0, 37 13, 00 23, 48 1, 02 -0, 46
4, 44 0, 91 -1, 73 0, 02 1, 48 -3, 45 -0, 75 -0, 65 -1, 03 -4, 94
-3, 95 -0, 89 5, 11 -2, 42 -1, 62 -0, 56 5, 37 1, 57 0, 01 2, 11
0, 08 -4, 05 0, 35 0, 71 0, 15 3, 29 -7, 35 -1, 05 -0, 57 0, 25
-0, 56 0, 08 29, 12 31, 60 0, 85 0, 32 0, 16 -0, 18 -4, 01 -1, 71
-0, 22 1, 05 -1, 50 0, 96 0, 85 1, 64 -0, 87 -2, 15 -0, 09 -0, 18
-2, 37 -1, 07 0, 12 -3, 08 -0, 24 -0, 99 1, 93 0, 17 4, 86 -2, 50

 

Вариант 7.

0, 97 0, 32 0, 31 0, 51 0, 48 0, 38 0, 11 0, 72 0, 60 0, 47
0, 07 0, 52 0, 05 0, 09 0, 11 0, 25 0, 98 0, 41 0, 00 0, 07
0, 36 6, 83 0, 62 0, 27 0, 63 0, 11 0, 36 1, 52 0, 24 0, 34
0, 04 0, 64 0, 55 0, 46 1, 55 0, 07 0, 05 1, 68 1, 55 0, 45
0, 37 0, 52 0, 27 0, 30 0, 03 3, 31 0, 09 0, 18 2, 64 0, 49
0, 89 0, 36 1, 37 0, 42 0, 04 0, 16 0, 20 0, 15 0, 08 1, 11
1, 54 0, 18 11, 29 0, 29 0, 12 0, 18 0, 28 0, 08 1, 47 2, 20
1, 08 3, 49 0, 64 0, 97 0, 03 0, 21 0, 90 4, 01 0, 38 0, 05
1, 05 0, 95 0, 91 1, 52 0, 15 0, 14 1, 12 1, 60 0, 29 0, 13
0, 56 2, 78 0, 11 25, 98 3, 13 0, 06 4, 14 1, 56 1, 37 0, 50

 

Вариант 8.

14, 78 5, 88 2, 03 8, 86 13, 16 7, 44 7, 81 11, 34 10, 38 13, 17
7, 00 12, 44 10, 86 12, 15 6, 44 13, 43 7, 94 4, 80 9, 55 4, 50
5, 01 11, 31 14, 26 6, 34 10, 13 7, 65 12, 01 5, 19 5, 69 17, 97
7, 30 7, 01 16, 28 12, 00 14, 82 2, 90 7, 18 9, 31 14, 23 12, 54
2, 38 9, 04 1, 73 17, 93 3, 03 4, 48 14, 27 14, 62 2, 16 13, 29
15, 87 5, 12 11, 18 12, 15 13, 23 10, 37 13, 40 16, 85 5, 65 17, 32
16, 93 17, 25 6, 81 13, 77 3, 16 10, 81 10, 26 9, 36 10, 68 4, 88
6, 24 18, 48 3, 15 6, 71 13, 40 22, 71 4, 75 4, 97 9, 08 11, 09
12, 92 5, 39 6, 64 9, 39 10, 70 5, 93 11, 35 3, 92 12, 22 4, 89
4, 18 4, 75 10, 97 24, 92 6, 85 6, 94 7, 21 13, 25 14, 35 1, 93

 

Вариант 9.

3, 36 0, 88 0, 62 0, 65 3, 95 2, 19 8, 10 2, 54 -5, 06 0, 85
6, 56 0, 63 0, 40 0, 37 0, 73 0, 16 0, 10 0, 43 1, 32 0, 94
-1, 47 2, 59 -2, 96 -2, 23 2, 51 0, 21 -3, 62 2, 24 2, 12 3, 59
0, 42 5, 47 2, 53 1, 36 0, 62 -1, 20 -1, 56 1, 68 4, 17 3, 66
1, 92 6, 12 1, 54 0, 00 2, 74 1, 69 0, 74 -0, 42 -0, 43 1, 75
0, 56 0, 63 -0, 92 -0, 62 3, 45 0, 98 2, 67 1, 48 -0, 29 -0, 55
1, 41 0, 10 0, 85 -0, 64 -0, 31 2, 28 2, 11 0, 76 1, 02 0, 28
2, 59 2, 80 -3, 72 3, 51 2, 83 -1, 26 0, 29 -0, 47 0, 65 -2, 78
0, 91 0, 95 -2, 47 -3, 63 -1, 62 -2, 04 0, 70 0, 86 -0, 60 2, 99
1, 18 1, 22 0, 31 -0, 42 4, 48 1, 00 1, 50 -1, 42 1, 34 0, 53

 

Вариант 10.

0, 98 0, 75 0, 96 2, 46 0, 39 0, 10 1, 68 1, 23 2, 93 1, 49
0, 46 0, 31 0, 94 0, 33 0, 67 2, 28 1, 40 1, 78 2, 28 1, 62
1, 35 0, 26 2, 20 1, 56 0, 36 0, 46 0, 62 1, 81 2, 16 1, 33
2, 14 0, 60 1, 12 1, 84 0, 94 0, 77 1, 02 0, 78 1, 25 0, 57
2, 08 0, 70 1, 05 2, 68 1, 16 1, 73 1, 27 0, 63 1, 18 2, 11
2, 52 0, 19 0, 85 1, 12 1, 20 1, 51 1, 58 2, 01 1, 50 0, 97
0, 17 0, 82 2, 73 0, 84 0, 97 1, 82 1, 27 0, 49 1, 16 0, 67
1, 02 0, 92 1, 81 1, 67 2, 92 1, 61 0, 63 0, 35 0, 56 0, 68
1, 99 1, 27 3, 08 0, 93 0, 29 0, 42 2, 65 1, 69 0, 28 0, 90
0, 55 0, 94 0, 77 1, 73 0, 72 0, 53 1, 52 1, 64 1, 78 0, 89

 

Вариант 11.

4, 95 6, 53 2, 35 2, 17 2, 31 0, 35 1, 76 2, 85 4, 75 1, 14
2, 88 2, 37 6, 41 1, 62 1, 27 3, 39 4, 71 2, 25 3, 22 1, 60
3, 24 2, 15 3, 50 3, 96 4, 20 4, 05 4, 96 5, 43 4, 16 4, 67
2, 40 3, 83 3, 40 1, 79 3, 21 8, 55 1, 99 4, 26 4, 29 3, 68
3, 22 3, 07 7, 26 8, 10 4, 76 1, 09 5, 31 4, 73 3, 80 3, 51
0, 48 3, 12 4, 30 3, 28 2, 34 1, 05 4, 96 8, 47 3, 00 3, 87
3, 26 7, 17 4, 46 1, 02 2, 86 0, 44 3, 12 4, 10 1, 29 0, 74
1, 32 3, 61 3, 07 2, 88 4, 13 6, 17 1, 06 1, 61 8, 57 3, 03
3, 86 3, 24 5, 02 5, 65 2, 89 9, 23 5, 79 4, 56 7, 22 1, 86
4, 61 7, 82 3, 39 2, 79 3, 97 2, 78 5, 20 1, 45 5, 87 1, 77

 

Вариант 12.

7, 39 0, 68 39, 45 16, 48 23, 22 1, 68 23, 75 0, 11 20, 11 6, 20
1, 18 2, 07 16, 35 0, 42 4, 42 4, 92 9, 58 17, 68 9, 43 7, 80
29, 68 2, 07 28, 11 8, 70 4, 03 0, 48 29, 81 4, 06 3, 37 1, 14
0, 58 2, 29 0, 29 7, 86 12, 44 9, 51 0, 25 0, 14 2, 84 10, 17
0, 73 3, 08 17, 88 6, 80 2, 10 24, 11 12, 23 11, 50 14, 08 27, 55
25, 40 13, 16 0, 63 20, 82 17, 36 10, 85 0, 60 1, 99 6, 85 1, 52
6, 42 25, 64 5, 00 3, 63 6, 01 0, 99 31, 46 14, 15 10, 97 5, 46
10, 90 6, 46 0, 11 0, 10 3, 23 5, 14 5, 98 8, 16 25, 54 17, 79
8, 41 2, 77 16, 77 2, 96 3, 22 1, 92 13, 03 19, 78 7, 51 8, 15
20, 61 14, 30 6, 17 23, 02 8, 52 13, 81 1, 65 5, 90 0, 67 21, 11

 

Вариант 13.

0, 03 0, 14 0, 02 0, 10 9, 47 0, 63 1, 04 2, 74 0, 08 0, 30
0, 08 0, 02 0, 29 0, 36 0, 50 0, 03 2, 61 0, 61 5, 44 3, 65
0, 14 0, 04 4, 72 0, 02 0, 01 0, 68 0, 06 0, 12 0, 20 1, 24
1, 49 0, 02 0, 08 0, 13 0, 02 0, 64 0, 46 0, 77 0, 28 0, 08
0, 75 0, 00 1, 70 0, 07 0, 11 2, 26 0, 05 1, 20 0, 47 0, 29
0, 24 2, 78 0, 13 1, 21 0, 75 2, 29 8, 23 0, 99 1, 98 0, 34
0, 72 0, 32 0, 10 0, 34 0, 84 0, 24 0, 82 0, 84 0, 18 1, 89
0, 15 0, 93 2, 05 6, 39 0, 07 0, 40 0, 15 0, 08 0, 40 0, 25
0, 54 0, 08 0, 05 0, 02 5, 68 0, 55 3, 08 0, 99 10, 61 1, 24
0, 60 0, 30 0, 04 0, 05 0, 81 0, 16 0, 05 2, 25 0, 35 0, 31

 

 

Вариант 14.

8, 62 -0, 04 13, 50 10, 30 8, 72 10, 86 5, 93 8, 84 6, 20 9, 78
7, 31 9, 41 4, 10 1, 36 9, 41 5, 37 6, 68 10, 51 8, 54 9, 46
8, 85 10, 73 7, 25 4, 19 13, 38 2, 83 9, 10 6, 85 4, 66 6, 24
5, 91 0, 53 9, 30 8, 47 8, 42 4, 33 9, 02 8, 99 3, 54 8, 92
7, 13 5, 78 8, 53 8, 33 6, 36 8, 69 11, 95 6, 30 10, 72 10, 33
14, 78 5, 88 11, 41 6, 27 5, 68 4, 99 11, 02 8, 27 13, 87 6, 54
5, 42 10, 02 6, 48 2, 11 3, 56 10, 00 8, 17 8, 19 10, 15 4, 69
10, 65 10, 00 8, 11 8, 58 8, 25 2, 67 7, 95 7, 65 7, 07 6, 65
7, 24 9, 46 1, 70 10, 51 8, 63 0, 96 7, 34 8, 69 3, 82 7, 75
7, 54 8, 29 7, 98 7, 45 14, 25 8, 15 4, 15 11, 53 5, 01 7, 28

 

Вариант 15.

0, 11 -1, 53 -0, 94 0, 21 0, 77 1, 10 0, 23 -0, 15 0, 79 -0, 71
1, 17 0, 01 0, 45 1, 55 1, 48 -0, 09 0, 01 1, 00 1, 25 1, 35
0, 52 -1, 61 2, 16 0, 64 0, 19 0, 02 0, 20 1, 43 0, 74 -0, 21
0, 41 0, 80 -0, 41 0, 31 -1, 26 0, 75 1, 05 2, 04 -0, 42 -1, 06
0, 33 -0, 30 -0, 34 -0, 10 -1, 54 0, 67 -0, 40 -0, 15 0, 98 -1, 04
1, 55 -1, 58 1, 78 -0, 71 0, 75 0, 48 -0, 18 0, 49 -0, 07 0, 90
1, 04 2, 75 1, 03 0, 76 -2, 53 0, 27 0, 92 -1, 17 -0, 85 -1, 83
-0, 35 -1, 07 -0, 02 1, 64 0, 35 -0, 86 -0, 06 0, 69 2, 16 -0, 54
1, 20 -0, 57 1, 57 -0, 05 0, 34 0, 83 -0, 28 0, 48 1, 85 0, 93
0, 91 -1, 50 -1, 08 0, 53 -0, 53 0, 29 0, 77 -1, 13 -0, 76 2, 30

 

Вариант 16.

7, 42 7, 97 10, 85 7, 65 5, 79 7, 62 5, 90 11, 17 8, 31 6, 79
6, 69 3, 12 5, 97 8, 61 3, 69 9, 43 12, 31 10, 46 10, 34 8, 76
9, 63 8, 83 7, 69 10, 17 7, 72 9, 99 3, 45 9, 95 8, 17 10, 74
7, 27 5, 81 6, 58 3, 74 7, 09 5, 20 2, 45 10, 62 4, 44 10, 24
4, 72 7, 88 5, 60 8, 83 9, 61 6, 60 5, 64 6, 34 7, 57 -1, 87
8, 14 10, 78 9, 91 11, 19 6, 74 5, 45 9, 51 3, 50 4, 08 5, 59
3, 45 12, 51 10, 86 8, 62 7, 22 7, 32 4, 04 8, 06 2, 81 7, 62
0, 59 6, 19 4, 89 6, 97 8, 36 7, 94 6, 82 7, 46 6, 62 8, 31
6, 07 8, 66 6, 60 8, 56 7, 09 3, 15 6, 62 7, 13 8, 78 8, 24
17, 94 12, 91 10, 80 1, 05 12, 64 7, 53 8, 62 7, 91 9, 09 5, 91

 

Вариант 17.

0, 50 0, 82 0, 80 3, 58 0, 20 1, 44 0, 64 0, 02 2, 04 0, 15
0, 88 0, 61 1, 55 0, 56 0, 28 0, 00 0, 62 0, 59 1, 56 1, 56
2, 58 0, 69 0, 12 1, 22 0, 64 0, 12 0, 76 0, 63 2, 48 1, 70
0, 10 4, 98 1, 06 0, 04 0, 33 0, 20 2, 13 0, 25 1, 05 2, 08
0, 44 0, 62 1, 16 0, 15 0, 02 0, 02 1, 27 0, 92 0, 29 0, 07
0, 15 1, 40 0, 89 0, 86 1, 39 0, 51 0, 26 0, 65 3, 93 0, 19
3, 31 0, 83 0, 20 2, 11 0, 26 3, 07 2, 34 0, 98 1, 26 0, 39
3, 08 0, 09 2, 02 6, 26 4, 76 2, 36 1, 41 0, 34 0, 17 0, 18
1, 82 3, 53 0, 49 1, 31 0, 63 0, 01 0, 42 4, 57 0, 55 1, 13
0, 79 2, 25 0, 66 1, 03 0, 94 0, 81 1, 29 2, 07 0, 09 2, 70

 

Вариант 18.

5, 70 11, 67 0, 99 3, 27 2, 27 9, 66 2, 21 15, 04 2, 68 6, 21
10, 48 9, 16 3, 29 12, 61 7, 17 6, 88 4, 92 3, 06 4, 97 5, 54
1, 62 9, 16 1, 76 5, 21 7, 43 12, 35 1, 61 7, 41 7, 91 10, 56
11, 98 8, 90 13, 34 5, 51 4, 12 4, 94 13, 62 14, 67 8, 36 4, 74
11, 52 8, 15 3, 02 5, 94 9, 12 2, 17 4, 17 4, 36 3, 75 1, 81
2, 03 3, 95 11, 81 2, 58 3, 11 4, 54 11, 91 9, 25 5, 92 9, 90
6, 11 2, 00 6, 83 7, 71 6, 30 10, 88 1, 48 3, 73 4, 51 6, 58
4, 53 6, 10 15, 03 15, 16 8, 02 6, 75 6, 32 5, 40 2, 01 3, 04
5, 31 8, 42 3, 22 8, 25 8, 03 9, 35 3, 98 2, 73 5, 65 5, 41
2, 61 3, 70 6, 22 2, 30 5, 27 3, 80 9, 70 6, 36 11, 70 2, 54

 

Вариант 19.

0, 97 0, 32 0, 31 0, 51 0, 48 0, 38 0, 11 0, 72 0, 60 0, 47
0, 07 0, 52 0, 05 0, 09 0, 11 0, 25 0, 98 0, 41 0, 00 0, 07
0, 36 6, 83 0, 62 0, 27 0, 63 0, 11 0, 36 1, 52 0, 24 0, 34
0, 04 0, 64 0, 55 0, 46 1, 55 0, 07 0, 05 1, 68 1, 55 0, 45
0, 37 0, 52 0, 27 0, 30 0, 03 3, 31 0, 09 0, 18 2, 64 0, 49
0, 89 0, 36 1, 37 0, 42 0, 04 0, 16 0, 20 0, 15 0, 08 1, 11
1, 54 0, 18 11, 29 0, 29 0, 12 0, 18 0, 28 0, 08 1, 47 2, 20
1, 08 3, 49 0, 64 0, 97 0, 03 0, 21 0, 90 4, 01 0, 38 0, 05
1, 05 0, 95 0, 91 1, 52 0, 15 0, 14 1, 12 1, 60 0, 29 0, 13
0, 56 2, 78 0, 11 25, 98 3, 13 0, 06 4, 14 1, 56 1, 37 0, 50

 

Вариант 20.

7, 85 1, 86 4, 19 5, 47 8, 23 4, 24 9, 30 9, 08 5, 68 5, 64
10, 54 5, 33 3, 08 3, 99 6, 61 10, 50 9, 27 7, 10 4, 72 8, 00
9, 94 7, 11 13, 96 2, 88 1, 28 9, 98 3, 76 6, 88 2, 15 2, 60
2, 21 9, 58 4, 43 1, 67 10, 24 4, 52 3, 49 6, 30 3, 49 9, 16
11, 01 5, 15 4, 78 1, 61 5, 38 6, 18 8, 18 6, 41 11, 49 5, 97
10, 15 3, 31 10, 21 7, 57 9, 18 4, 20 8, 43 10, 56 1, 44 14, 36
4, 25 2, 77 10, 02 7, 82 9, 04 2, 68 1, 97 1, 19 9, 48 5, 19
7, 37 5, 75 4, 77 2, 24 5, 88 7, 84 4, 01 3, 80 3, 85 4, 04
14, 38 2, 31 4, 32 5, 91 6, 86 3, 02 3, 98 10, 63 2, 64 14, 44
5, 04 7, 12 9, 09 8, 97 5, 60 4, 65 5, 40 6, 76 9, 76 6, 17

 

 


⇐ Предыдущая1234
Поделиться с друзьями:
mylektsii.su - Мои Лекции - 2015-2024 год. (0.021 сек.)Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав Пожаловаться на материал