Критерий (Пирсона) для сложной гипотезы

Пусть 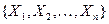выборка из генеральной совокупности 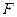. Проверяется сложная гипотеза 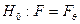, где 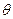- неизвестный параметр распределения 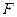(или вектор параметров), против альтернативы .

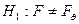Пусть выборка по прежнему представлена в виде группированного ряда и 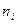- число элементов выборки попавших в 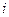-ый интервал, 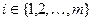. Статистику (1) мы не можем в этом случае использовать для построения критерия Пирсона, так как не можем вычислить теоретические значения вероятностей 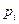, которые зависят от неизвестного параметра 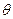. Пусть 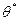- оценка параметр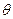а , а 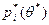- соответствующие ей оценки вероятностей 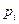. Составим статистику .

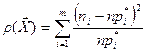Теорема Пирсона. Если 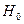верна, и 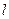- число компонент вектора 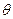(число неизвестных параметров распределения), то при фиксированном 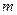и

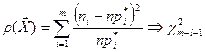. (3)

Таким образом, критерий Пирсона для параметрической гипотезы будет иметь вид:

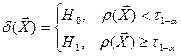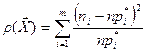, , (4)

где 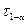- квантиль распределения .

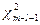Замечание. Вообще говоря, оценки, используемые для построения статистики критерия хи-квадрат, должны быть определены из условия минимума статистики 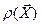. Поэтому желательно уточнить оценки, найденные другим способом (методом максимального правдоподобия или методом моментов) путем минимизации .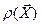