
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Показатели метрологической надежности средств измерений
|
|
В технике используется большое число показателей надежности, которые приведены в стандарте ГОСТ 27.002-89 " Надежность в технике. Термины и определения". Рассмотрим основные из них, нашедшие применение в теории метрологической надежности. Знание показателей метрологической надежности позволяет потребителю оптимально использовать СИ, планировать мощности ремонтных участков, размер резервного фонда приборов, обоснованно назначать межповерочные интервалы и грамотно проводить мероприятия по техническому обслуживанию СИ.
Стабильность СИ характеризуется плотностью распределения приращения погрешности Δ [Δ (t)] = Δ 0, 95(t) – Δ 0.
Среди показателей безотказности наибольшее распространение получили вероятность безотказной работы, средняя и гаммапроцентная наработки до отказа и интенсивность отказов. Вероятность безотказной работы СИ Р(t) — это вероятность того, что в течение времени * нормированные МХ не выйдут за допускаемые пределы, т.е. не наступит метрологический отказ. Наработкой называется продолжительность работы СИ, а наработкой до отказа — продолжительность работы от начала эксплуатации до возникновения первого отказа.
Вероятность Р(t) является функцией времени и задается аналитически либо таблицей или графиком. Например, если вероятность безотказной работы в течение 1000 ч составляет Р(t) = 0, 97, то это означает, что в среднем из большого числа СИ данного типа около 97% проработают более 1000 ч. Вероятность Р(t) изменяется от нуля до единицы. Чем она ближе к единице, тем выше безотказность работы СИ. На практике допустимым считается значение Р(t) ≥ 0, 9. Вероятность безотказной работы СИ в интервале от 0 до t определяется по формуле
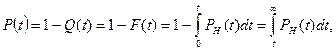
где F(t), pн(t) — интегральная и дифференциальная функции распределения наработки на отказ; Q(t) — вероятность отказа.
Средней наработкой до отказа называется математическое ожидание наработки СИ до первого отказа:
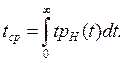
Гамма-процентная наработка до отказа tγ — это наработка, в течение которой отказ объекта не возникает с вероятностью у, выра-женной в процентах. Она определяется из уравнения
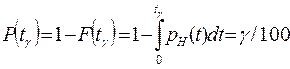
При γ = 100% гамма-процентная наработка называется установлен-ной безотказной наработкой, а при γ = 50% — медианной наработкой.
Частота (интенсивность) отказов ω (t) определяется как условная плотность вероятности возникновения отказа невосстанавливаемого СИ, которая находится для рассматриваемого момента времени при условии, что до этого момента отказ не возник:
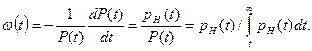
Вероятность того, что СИ, проработавшее безотказно в течение времени t, откажет в последующий малый промежуток времени dt, равна ω (t)dt. Вероятность безотказной работы выражается через интенсивность отказов следующим образом:
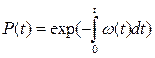
Из теории надежности известно, что при постепенных отказах, к которым относятся и метрологические отказы, плотность распределения наработки на отказ распределяется в основном по одному из четырех законов: экспоненциальному, нормальному, логнормальному и закону Вейбулла. Выбор того или иного закона должен производиться только на основе экспериментальных исследований. При нормальном законе
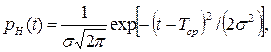
где Тср, σ — параметры распределения. В этом случае
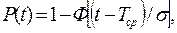
где Ф(z) — функция Лапласа.
Интенсивность отказов описывается выражением

Для использования этих формул необходимо знать средний срок службы ТСР и его СКО σ, которые находятся экспериментально при испытаниях СИ на надежность.
Основными показателями долговечности являются средние и гамма-процентные сроки службы и ресурсы. Срок службы — это календарная продолжительность работы СИ от начала его эксплуатации до перехода в предельное состояние. Он измеряется в годах или месяцах. Средним сроком службы называется математическое ожидание срока службы

где fСЛ(t) — плотность распределения срока службы для совокупности СИ данного типа.
Гамма-процентный срок службы — это календарная продолжительность от начала эксплуатации СИ, в течение которой оно не достигнет предельного состояния с заданной вероятностью γ, выраженной в процентах. Он определяется из уравнения
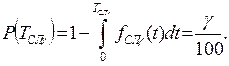
Ресурсом называется наработка СИ от начала его эксплуатации до перехода в предельное состояние. Ресурс представляет собой запас возможной выработки СИ. Средним ресурсом называется математическое ожидание ресурса

где fP(t) — плотвость распределения ресурса для совокупности СИ данного типа.
Гамма-процентный ресурс — это наработка, в течение которой средство измерений не достигнет своего предельного состояния с заданной вероятностью γ, выраженной в процентах. Он определяется из уравнения
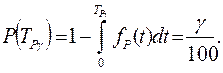
Срок службы (средний или гамма-процентный) акцентирует внимание на календарной продолжительности эксплуатации, включая в себя, помимо времени непосредственной работы СИ, время хранения его ва складе, нахождения в выключенном состоянии, транспортировку, ремонт и т.д. При нормировании он задается в годах. Ресурс (средний или гамма-процентный) представляет собой чистую наработку изделия, находящегося во включенном состоянии, и нормируется в часах.
В табл. 1 приведены показатели безотказности и долговечности некоторых электронных СИ по данным заводов-изготовителей. При анализе этих данных следует помнить, что они характеризуют суммарную надежность (метрологическую и неметрологическую). Однако метрологические отказы при эксплуатации СИ составляют более 60% на третьем году эксплуатации и достигают 96% при работе более четырех лет. Поэтому приведенные данные в значительной степени относятся к метрологической надежности.
Таблица 1.