
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вариационное исчисление
|
|
S-domain описание
· Передаточная функция
Ширяева О.И.
КазНТУ им.К.Сатпаева
Осень, 2013
Пусть система управления описывается блок-схемой:
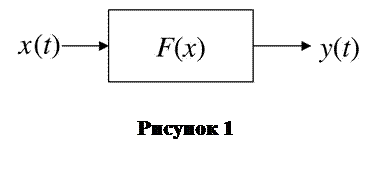
где x (t) - входной сигнал,
y (t) - выходной сигнал.
|
Вариационное исчисление
Представление в комплексной плоскости предоставляет математическое описание для анализа и синтеза систем. Во-первых, введем комплексную переменную

 , оператор Лапласа
, оператор Лапласа
где j - комплексная величина.

 Преобразование по Лапласу преобразовывает любой временной сигнал (оригинал),
Преобразование по Лапласу преобразовывает любой временной сигнал (оригинал), 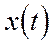 ,
,
 в сигнал комплексной области (изображение) X (s):
в сигнал комплексной области (изображение) X (s):
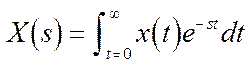 (1.1)
(1.1)
где функция X(s) называется " преобразование по Лапласу входного сигнала 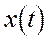 ".
".
Прямое преобразование символически обозначается как 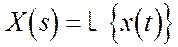 , может быть выполнено для любого сигнала
, может быть выполнено для любого сигнала 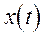 , который удовлетворяет условию:
, который удовлетворяет условию:

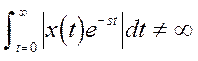 (1.2)
(1.2)
 Когда сигнал X (s) определен, то его то его оригинал можно определить с помощью " обратного преобразования по Лапласу"
Когда сигнал X (s) определен, то его то его оригинал можно определить с помощью " обратного преобразования по Лапласу" 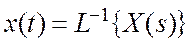 :
:
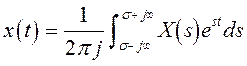 (1.3)
(1.3)
where s is a real constant.
Каково объяснение преобразования по Лапласу? Те, кто помнит анализ Фурье, должны вспомнить, что это преобразование может рассматриваться как техника для представления непрерывно–временного сигнала комбинацией гармонических составляющих следующим образом:
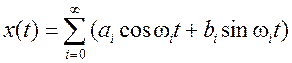 , (1.4)
, (1.4)
и преобразование Фурье 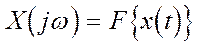 , в основном определяет коэффициенты
, в основном определяет коэффициенты 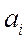 и
и 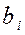 для каждой частоты
для каждой частоты 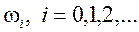 Точно так же преобразование по Лапласу, может рассматриваться как техника для представления сигнала x (t) временной области совокупностью экспоненциально затухающих гармонических составляющих:
Точно так же преобразование по Лапласу, может рассматриваться как техника для представления сигнала x (t) временной области совокупностью экспоненциально затухающих гармонических составляющих:
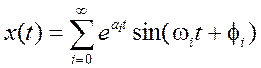 , (1.5)
, (1.5)
и, поэтому, преобразование по Лапласу 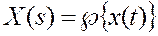 определяет параметр затухания
определяет параметр затухания  , и сдвиг по фазе
, и сдвиг по фазе 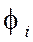 для каждой частоты
для каждой частоты 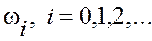 . Это, однако, не объясняет использование преобразование по Лапласу. Данное использование стало важным из–за множества свойств, которые являются чрезвычайно полезными, когда задача связана с линейными дифференциальными уравнениями высокого порядка.
. Это, однако, не объясняет использование преобразование по Лапласу. Данное использование стало важным из–за множества свойств, которые являются чрезвычайно полезными, когда задача связана с линейными дифференциальными уравнениями высокого порядка.