
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. 1. Рассмотрим сначала случай a > 1
|
|
Преобразуем:
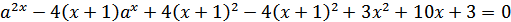

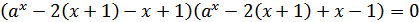
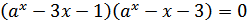
Таким образом:
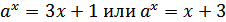
1. Рассмотрим сначала случай a > 1
Прежде всего, уравнение (1) всегда имеет корень х=0, который от значения параметра не зависит. Тогда для выполнения условия задачи надо, чтобы либо уравнение (1) имело еще один корень на указанном промежутке, а уравнение (2) – нет, либо чтоб уравнение (2) имело один корень на этом промежутке, а уравнение (1) – нет. Условия составим на основе сравнения значений функций на границах промежутка.
1. уравнение (1) имеет корень на указанном промежутке, а уравнение (2) – нет:
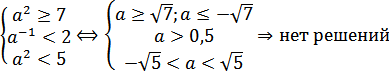
2. уравнение (2) имеет один корень на этом промежутке, а уравнение (1) – нет:
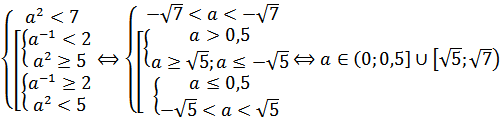
Первый промежуток не удовлетворяет условию a > 1. Значит 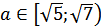 .
.
Также возможен случай если в уравнении (1) прямая является касательной к графику показательной функции:
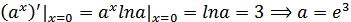
Тогда уравнение (2):
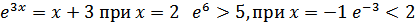
то есть корень попадает в рассматриваемый промежуток.
2. Теперь рассмотрим случай 0 < a < 1
Так как функция 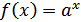 – убывающая, а линейные функции – возрастающая, то здесь каждое уравнение имеет один корень. Причем уравнение (1) всегда имеет корень х = 0 не зависимо от а. Значит для выполнения условия задачи корень уравнения (2) должен попасть в отрезок [-1; 2]:
– убывающая, а линейные функции – возрастающая, то здесь каждое уравнение имеет один корень. Причем уравнение (1) всегда имеет корень х = 0 не зависимо от а. Значит для выполнения условия задачи корень уравнения (2) должен попасть в отрезок [-1; 2]:
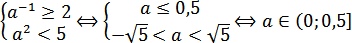
Теперь рассмотрим случай совпадения корней:
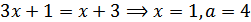
Ответ: 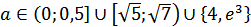
C5 Найдите все значения параметра а, при каждом из которых уравнение 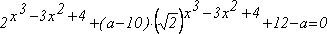 имеет шесть корней.
имеет шесть корней.