
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Абсолютная погрешность.
|
|
Для характеристики степени приближения к истинному значению вводится понятие абсолютной погрешности — величины, показывающей, насколько найденное численное значение может отличаться от истинного значения измеряемой величины. Абсолютнаяпогрешность измеряется в тех же единицах, что и измеряемая величина. При многократных измерениях какой-либо величины различают среднюю абсолютную погрешность отдельного измерения и абсолютную погрешность среднего арифметического, полученного из всей серии многократных измерений. Результат, получаемый как среднее арифметическое из всей серии многократных измерений, тем надежнее, чем больше сделано измерений. Поэтому абсолютная погрешность результата ряда многократных измерений меньше абсолютной погрешности отдельного измерения, и тем меньше, чем больше число выполненных измерений.
Под средней абсолютной погрешностью отдельного измерения понимается среднее арифметическое из всех величин отклонений каждого отдельного измерения от среднего арифметического. Если обозначить величины отклонений 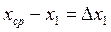 ,......,
,......,  , то средняя абсолютная погрешность отдельного измерения в серии из п измерений выражаетсям как
, то средняя абсолютная погрешность отдельного измерения в серии из п измерений выражаетсям как
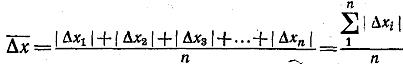 , (2)
, (2)
где все величины | ∆ хi | представляют собой абсолютные значения отклонений от среднего арифметического, т. е. взятые все с положительными знаками.
Для средней абсолютной погрешности среднего арифметического серии многократных измерений теория приближенных вычислений дает выражение:
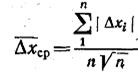 , (3)
, (3)
показывающее, что с увеличением числа измерений эта погрешность уменьшается, будучи обратно пропорциональной квадратному корню из числа измерений.
При многократных измерениях чаще используется понятие средней квадратичной погрешности измерений, причем в этом случае также различают среднюю квадратичную погрешность отдельного измерения и среднюю квадратичную погрешность результата, полученного из серии всех измерений.
Средняя квадратичная погрешность для отдельного измерения (стандартное отклонение):
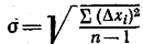 , (4)
, (4)
Средняя квадратичная погрешность для результата серии измерений:
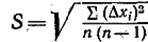 , (5)
, (5)