
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
При косвенных измерениях
|
|
Часто для вычисления какой-либо величины требуется измерить ряд других величин. Так, мощность постоянного тока, измеряемая с помощью амперметра и вольтметра, вычисляется как произведение Р = IU. В таких случаях необходимо уметь вычислить погрешность в определении искомой величины, если известны погрешности непосредственно измеряемых величин, функцией которых она является. Очевидно, погрешность в таком косвенном измерении некоторой величины определенным образом слагается из погрешностей в величинах, измеряемых непосредственно.
Приведем примеры нахождения погрешностей в двух случаях — когда она является разностью д в у х измеряемых величин или их произведением.
1. Искомая величина — разность двух измеряемых величин: N = а — в. Напишем выражение разности между разностью измеренных величин с их погрешностями и разностью этих же величин без погрешностей. Но здесь следует положить, во избежание преуменьшения величины погрешности, что погрешности в измерении уменьшаемого и вычитаемого противоположны по знаку:
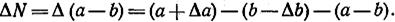
Отсюда получим
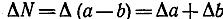 , (7)
, (7)
Рассуждая аналогично, легко получить выражение абсолютной погрешности для случая, когда N = а + b:
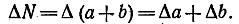
Таким образом, абсолютная погрешность суммы или разности двух измеряемых величин равна в обоих случаях сумме абсолютных погрешностей этих величин.
Относительная погрешность в этих случаях выразится так:
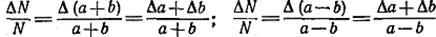 , (8)
, (8)
2.Искомая величина — произведение двух измеряемых величин: N = а ∙ b. В этом случае
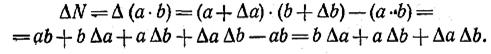
Так как величина ∆ а∆ b очень мала — она представляет собой произведение двух малых величин, — то ею можно пренебречь. Тогда абсолютная погрешность произведения выразится формулой
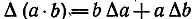 , (9)
, (9)
Относительная погрешность произведения
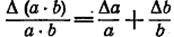 , (10)
, (10)
т. е. равна сумме относительных погрешностей сомножителей. Аналогично можно получить выражение для относительной погрешности дроби (частного):
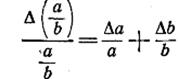 , (11)
, (11)
т. е. она равна сумме относительных погрешностей числителя и знаменателя, подобно тому, как это было для произведения.