Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Построение графиков и определение погрешностей по ним
|
|
Во многих лабораторных работах оказывается, удобным изображать графически зависимость между изучаемыми величинами. Для того, чтобы построить график, необходимо на основании проделанных измерений составить таблицу, в которой каждому значению одной из величин соответствует определенное значение другой. Для правильного построения графика весьма важным является целесообразный выбор масштаба. Масштаб по каждой оси может быть свой, причем выбирать его следует так, чтобы пределы изменений обеих величин ограничивали на осях отрезки примерно одинаковые по величине, иначе график может оказаться очень сжатым по одной из осей и неудобным для пользования. Если первое значение измеряемой величины сильно отличается от нуля и, особенно, если изменение этой величины невелико, отсчет в начале координат нужно начинать не от нуля, а от какого-то значения, близкого к первому измеренному значению данной величины. Когда масштаб выбран, нужно разделить оси в выбранном масштабе на равные интервалы и надписать на осях значения этих интервалов (рис. 1). После этого на график наносят точки на основании данных таблицы и проводят через них прямую или плавную кривую линию.
Так как все измерения сделаны с той или иной ошибкой, то может иметь место некоторый разброс точек (они не укладываются точно на одной кривой). В этом случае линию нужно проводить между точками так, чтобы возможно большее число точек легло на эту линию, а остальные распреде
лились примерно равномерно выше и ниже ее (рис. 1). С помощью полученного графика можно для любого промежуточного значения одной из величин найти соответствующее ему значение другой величины.
Если при построении графика наблюдается значительный разброс точек, то погрешность можно определить сле дующим образом. Нужно измерить отклонение каждой экспериментальной точки от линии графика по направлению, параллельному той оси, вдоль которой отложена интересующая нас величина, и найти среднее значение этого отклонения. В качестве примера рассмотрим вычисление погрешности по графику, изображенному на рис. 1.

Рис.1
На этом графике представлена зависимость оптической плотности раствора от концентрации. Для того, чтобы с помощью этого графика найти погрешность в определении концентрации, нужно измерить в масштабе все значения ∆ С, затем сложить их и разделить на число точек:
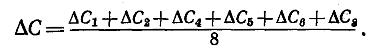
Такой способ нахождения погрешности удобен при наличии значительного разброса точек. Если же разброс точек невелик, что можно использовать другой способ определения погрешности по графику. На основании графика можно найти абсолютную ошибку в определении одной величины, если известна абсолютная ошибка в определении другой величины. Пусть график изображает зависимость величины у от величины х. Если какое-то значение величины х измерено с ошибкой ∆ х, то надо на соответ ствующей оси около этого значения х отложить отрезок ∆ х в выбранном масштабе и по графику найти соответствующий ему отрезок ∆ у на другой оси. Найденный отрезок ∆ у и будет представлять собой абсолютную ошибку в определении интересующего нас значения величины у. В случае прямолинейного графика ошибка, определенная таким образом, во всех его точках одинакова. Если же график представляет собой кривую линию, то ошибка на разных его участках будет различной.
В качестве примера графического вычисления ошибки разберем определение концентрации окрашенного раствора по величине его оптической плотности. В этой работе сначала измеряется оптическая плотность D нескольких растворов с известной концентрацией С и на основании этих данных строится график зависимости оптической плотности от концентрации (рис. 2). Затем измеряется величина оптической плотности Dх раствора неизвестной концентрации. Пусть, она была измерена 3 раза и оказалась равной: 0, 76, 0, 78 и 0, 75. Тогда среднее значение Dхср = 0, 76, а средняя абсолютная ошибка ∆ Dх ср = 0, 0 1.
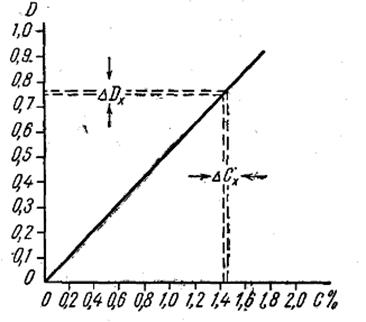
Рис.2
По графику находят значение концентрации, соответствующее среднему значению оптической плотности Dхср. В нашем случае Сх равно 1, 42%. Около значения Dхср на оси ординат откладывают отрезок, равный ∆ Dх ср и по графику находят, какой отрезок соответствует ему на другой оси. Этот отрезок и даст среднюю абсолютную ошибку в опреределении искомой концентрации. Как видно из рис. 2, ∆ Сх равно 0, 02. Тогда окончательный результат запишется так: