Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчет сетевых характеристик РСеМО
|
|
Сетевые характеристики, описывающие эффективность функционирования СеМО в целом, рассчитываются на основе полученных значений узловых характеристик.
В состав сетевых характеристик входят:
• среднее число заявок, ожидающих обслуживания в сети, и среднее число заявок, находящихся в сети:
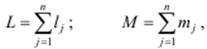
где lj – средняя длина очереди и mj – среднее число заявок в узле j;
• среднее время ожидания и среднее время пребывания заявок в сети:
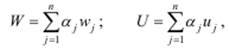
где wj и uj – соответственно среднее время ожидания и среднее время пребывания заявок в узле j; α j – коэффициент передачи для узла j, показывающий среднее число попаданий заявки в узел j за время ее нахождения в сети.
Пример 4.2. Проиллюстрируем изложенный метод расчета характеристик функционирования линейных разомкнутых однородных экспоненциальных СеМО на примере СеМО с четырьмя узлами (n = 4), граф которой представлен на рис.4.12. Связи между узлами СеМО описываются следующей матрицей вероятностей передач: 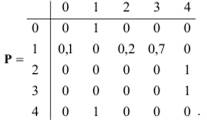
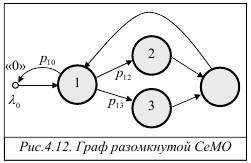
В РСеМО поступает простейший поток заявок с интенсивностью λ 0 = 0, 1с− 1 Положим, что все узлы СеМО – одноканальные, а средние длительности обслуживания заявок в узлах соответственно равны: b1= 0, 8 с; b2 = 2 с; b3 = 0, 4 с; b4 = 0, 3с.
Система линейных алгебраических уравнений для расчёта интенсивностей потоков заявок в узлах СеМО, согласно (4.16), имеет вид:
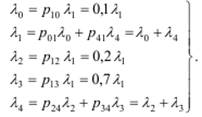
Решая эту систему уравнений, получим следующие значения интенсивностей: λ 1 =1с− 1, λ 2 = 0, 2 с− 1, λ 3 = 0, 7 с− 1, λ 4 = 0, 9 с− 1. Тогда коэффициенты передач будут равны: α 1 = λ 1 / λ 0 =10; α 2 = λ 2 / λ 0 = 2; α 3= λ 0 / λ 3 = 7; α 4 = λ 4 / λ 0 = 9.
Определим предельную интенсивность поступления заявок в разомкнутую СеМО, при которой в сети отсутствуют перегрузки. Для этого воспользуемся выражением (3.25), определяющим условие отсутствия перегрузок в РСеМО:
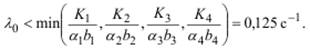
РСеМО работает без перегрузок, поскольку данное условие выполняется.
В соответствии с эквивалентным преобразованием представим рассматриваемую экспоненциальную разомкнутую СеМО в виде 4-х независимых СМО типа M/M/1, в которые поступают простейшие потоки заявок соответственно с интенсивностями: λ 1 = 1с− 1, λ 2 = 0, 2 с− 1, λ 3=0, 7с− 1, λ 4 = 0, 9 с− 1, а средние длительности обслуживания заявок в СМО совпадают с длительностями обслуживания в соответствующих узлах СеМО: b1 = 0, 8 с; b2 = 2с; b3 = 0, 4 с; b4 = 0, 3с.
Значения узловых характеристик СеМО, рассчитанные с использованием выражения (4.1) для среднего времени ожидания заявок в очереди СМО типа M/M/1 и фундаментальных соотношений, представленных в п.3.4.3, приведены в табл.4.1.
Таблица 4.1

В табл.4.2 представлены математические зависимости и полученные на их основе значения сетевых характеристик, рассчитанные с учётом найденных значений узловых характеристик.
Таблица 4.2