Свойства случайных ошибок измерений

Теория ошибок изучает только случайные ошибки. Под случайной ошибкой здесь и далее будем понимать разность

Δ i = Х – ℓ i

гдеΔ i – истинная случайная ошибка; Х – истинная величина; ℓ i – измеренная величина.

Случайные ошибки имеют следующие свойства:

1. Чем меньше по абсолютной величине случайная ошибка, тем она чаще встречается при измерениях.

2. Одинаковые по абсолютной величине случайные ошибки одинаково часто встречаются при измерениях.

3. При данных условиях измерений величина случайной погрешности по абсолютной величине не превосходит некоторого предела. Под данными условиями подразумевается один и тот же прибор, один и тот же наблюдатель, одни и те же параметры внешней среды. Такие измерения называют равноточными.

4. Среднее арифметическое из случайных ошибок стремиться к нулю при неограниченном возрастании числа измерений.

Три первых свойства случайных ошибок достаточно очевидны. Четвертое свойство вытекает из второго.

Если Δ 1, Δ 2, Δ 3,..., Δ n - случайные ошибки отдельных измерений, где n – число измерений, то четвертое свойство случайных ошибок математически выражается

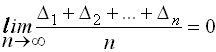
Предел этого отношения будет равен нулю, потому что в числителе сумма случайных ошибок будет конечной величиной, так как положительные и отрицательные случайные ошибки при сложении будут компенсироваться.

Чтобы запись была компактной, Гаусс предложил сумму записывать символом

,

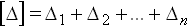тогда