
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Неделя 9. Лекция 9.4.2015
|
|
Теорема 2. Линейная комбинация решений линейного однородного дифференциального уравнения тоже является его решением.
Теорема 3. (Теорема о наложении решений). Если y1 - решение линейного неоднородного дифф.уравнения с правой частью b1(x), а y2 - решение такого же дифф.уравнения, но с правой частью b2(x), то линейная комбинация Ay1 + By2 является решением уравнения с правой частью Ab1(x) + Bb2(x).
Следствие. Сумма решений линейного неоднородного и соответствующего однородного дифференциального уравнения является решением неоднородного уравнения.
Определение линейной зависимости и независимости. Определитель Вронского.
Примеры. x, 2x x, x2.
Основное свойство. 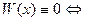 система функций линейно-зависима.
система функций линейно-зависима.
Теорема 4. Существует ровно n линейно-независимых решений линейного однородного дифф. уравнения порядка n, всякое решение есть их линейная комбинация.
Определение. Система из n решений, указанная в этой теореме, называется ФСР (фундаментальной системой решений) линейного однородного дифф. уравнения.
3 случая: случай 1 - все характеристические корни действительные и различные
(док, что система 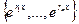 линейно независима.)
линейно независима.)
Линейные однородные. Примеры. 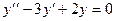 ,
,  .
.
случай 2 - все характеристические корни действительные, но среди них есть кратные
Система 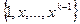 линейно независима и входит в ФСР однородного уравнения, если 0 есть корень кратности k.
линейно независима и входит в ФСР однородного уравнения, если 0 есть корень кратности k.
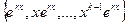 входит в ФСР однородного уравнения, если r есть корень кр-сти k.
входит в ФСР однородного уравнения, если r есть корень кр-сти k.
Пример. 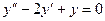 .
.
случай 3 - есть комплексные характеристические корни.
Если корень a+bi, то в ФСР входят две функции: 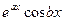 и
и 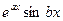 . Пример.
. Пример. 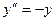 .
.