Неделя 11. Лекция 23.4.2015

Объединение и пересечение (сумма и произведение событий).

Сначала на примере геометрических множеств. .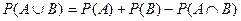

Пример. Схема с параллельным соединением, вероятность исправности 0, 9 и 0, 8 соответственно. Найти вероятность, что ток пройдёт. Отв. 0, 98. Разные подходы. Либо 0, 9 + 0, 8 от оставшегося периода времени (0, 1) либо по формуле .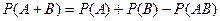

§ 2. Условная вероятность. Формула Байеса.

Условная вероятность: 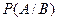- вероятность события А при условии, что выполнено B.

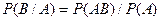, тогда 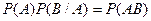. Аналогично .

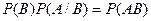Пример. В одной коробке 2 белых шара и 1 чёрный, во второй 1 белый и 2 чёрных.

Если произошло событие Н₁ - выбрана 1-я коробка, то вероятность выбрать белый шар 2/3.

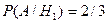. А выбрать белый шар из 2-й коробки .

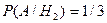Пример. 3 белых и 2 чёрных шара. Событие А - на 1-м шаге выбран белый. Событие В - на 2-м шаге выбран белый. Вероятность, что первые 2 выбранных шара белые, это = .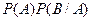

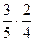Пример. Есть 20 машин - 10 грузовых и 10 легковых. Из 10 легковых 2 покрашены в зелёный цвет.

Вероятность выбрать зелёную машину P(A) = 2/20, но если изначально есть событие В (выбрали только легковые) то P(A/B) = 2/10.

ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ.

.

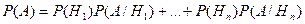Пример. В одной коробке 2 белых шара и 1 чёрный, во второй 1 белый и 2 чёрных. С вероятностью 3/4 выбирается 1-я коробка, с вероятностью 1/4 вторая. Найти вероятность взять белый шар.

.

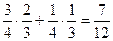Апостериорные вероятности и ФОРМУЛА БАЙЕСА.

Верны 2 формулы: 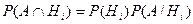и .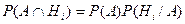

тогда можно вычислить - вероятность, что событие А произошло именно при исходном Н_i.

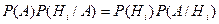тогда 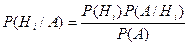, а с помощью ф-лы полной вер-сти:

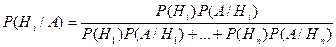- формула Байеса.

Пример. В одной коробке 1 белый шар и 2 чёрных, во второй все 3 белых. Взяли шар из какой-то коробки, и он оказался белый. Найти вероятность, что это был шар именно из 1-й коробки.

P(H₁) = P(H₂) = 1/2. P(A/H₁) = 1/3. P(A/H₂) = 1. Надо найти P(H₁/A).

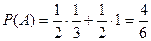. И действительно, замечаем, что белых шаров 4 из 6.

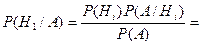
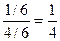. Интерпретация того, что мы нашли, смысл величины P(H₁/A): белых шаров, которые именно в 1-й коробке - 1 из 4 имеющихся в двух коробках, и вероятность что вытащили именно этот шар, 1/4.

§ 3. Схема Бернулли. Теоремы Муавра-Лапласа.

Пусть проводится серия n независимых экспериментов, вероятность наступления некоторого события p. Вероятность, что оно не наступило, q = 1-p. Найти вероятность того, что при n испытаниях оно наступит ровно m раз.

.

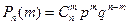Пример. Производится 3 выстрела по мишени, вероятность каждого попадания 1/4. Найти вероятности, что произошло 0, 1, 2, 3 попаданий.

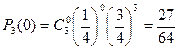
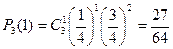
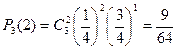
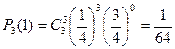
P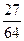

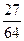
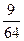
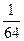
Неделя 12. Лекция 30.4.2015 теоремы Муавра-Лапласа, поток Пуассона.