НЕОДНОРОДНЫЕ системы.

Метод Лагранжа для линейного неоднородного уравнения порядка n, построение системы для неизвестных. Система, из которой находятся неизвестные функции:

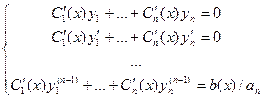
Пример. Решение методом Лагранжа уравнения

Сначала решается соответствующее однородное уравнение .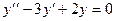

Его характеристическое уравнение это 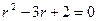, корни равны 1 и 2, общее решение однородного 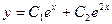.Далее вместо констант ставим неизвестные функции, то есть решение неоднородного ищем в виде 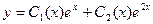. Для того, чтобы найти неизвестные функции, строим систему:

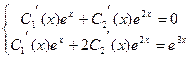
Решая её методом Гаусса, находим производные, а затем и сами функции и подставляем их в выражение 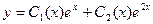. Приводя подобные, в итоге получим: .

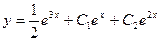Метод неопределённых коэффициентов для неоднородного уравнения.

Для 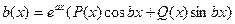частное решение неоднородного ищем в виде

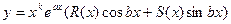
Примеры. (3 не совпадает ни с каким хар. корнем)

и 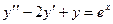(1 совпадает с хар. корнем кратности 2)