Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Изобразить схему замещения 3-фазного источника в случае соединения его фаз “треугольником”. Привести векторную топографическую диаграмму напряжений такого источника.
|
|
Ответ: При соединении источника питания треугольником (рис. 3.12) конец X одной фазы соединяется с началом В второй фазы, конец Y второй фазы – с началом С третьей фазы, конец третьей фазы Z – c началом первой фазы А. Начала А, В и С фаз подключаются с помощью трех проводов к приемникам.
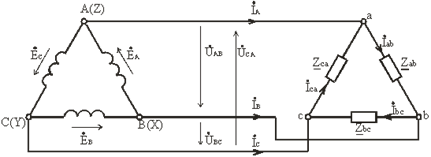Рис. 3.12
Соединение фаз источника в замкнутый треугольник возможно при симметричной системе ЭДС, так как: Ė A + Ė B + Ė C = 0. (3.17). Если соединение обмоток треугольником выполнено неправильно, т.е. в одну точку соединены концы или начала двух фаз, то суммарная ЭДС в контуре треугольника отличается от нуля и по обмоткам протекает большой ток. Это аварийный режим для источников питания, и поэтому недопустим. Напряжение между концом и началом фазы при соединении треугольником – это напряжение между линейными проводами. Поэтому при соединении треугольником линейное напряжение равно фазному напряжению. UЛ = UФ. (3.18). Пренебрегая сопротивлением линейных проводов, линейные напряжения потребителя можно приравнять линейным напряжениям источника питания: Uab = UAB, Ubc = UBC, Uca = UCA. По фазам Zab, Zbc, Zca приемника протекают фазные токи İ ab, İ bc и İ ca. Условное положительное направление фазных напряжений Ú ab, Ú bc и Ú ca совпадает с положительным направлением фазных токов. Условное положительное направление линейных токов İ A, İ B и İ C принято от источников питания к приемнику. В отличие от соединения звездой при соединении треугольником фазные токи не равны линейным. Токи в фазах приемника определяются по формулам: İ ab = Ú ab / Z ab; İ bc = Ú bc / Z bc; İ ca = Ú ca / Z ca. (3.19). Линейные токи можно определить по фазным, составив уравнения по первому закону Кирхгофа для узлов a, b и c (рис 3.12): İ A = İ ab - İ ca; İ B = İ bc - İ ab; İ C = İ ca - İ bc. (3.20). Сложив левые и правые части системы уравнений, (3.20), получим: İ A + İ B + İ C = 0, (3.21)
т.е. сумма комплексов линейных токов равна нулю как при симметричной, так и при несимметричной нагрузке. Симметричная нагрузка: При симметричной нагрузке:
Z ab = Z bc = Z ca = Z ejφ , (3.22) т.е. Zab = Zbc = Zca = Z, φ ab = φ bc = φ ca = φ. Так как линейные (они же фазные) напряжения UAB, UBC, UCA симметричны, то и фазные токи образуют симметричную систему: İ ab = Ú ab / Z ab; İ bc = Ú bc / Z bc; İ ca = Ú ca / Z ca. Абсолютные значения их равны, а сдвиги по фазе относительно друг друга составляют 120°. Линейные токи: İ A = İ ab - İ ca; İ B = İ bc - İ ab; İ C = İ ca - İ bc; образуют также симметричную систему токов (рис.3.13, 3.14).
Рис. 3.13
На векторной диаграмме (рис. 3.14) фазные токи отстают от фазных напряжений на угол φ (полагаем, что фазы приемника являются индуктивными, т.е. φ > 0°). Здесь принято, что напряжение UAB имеет нулевую фазу. Из диаграммы следует, что любой линейный ток больше фазного в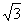 
раз. Линейный ток İ A отстает по фазе от фазного тока İ ab на угол 30°, на этот же угол отстает İ B от İ bc, İ C от İ ca. Таким образом, при соединении треугольником действующее значение линейного тока при симметричной нагрузке в 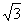раз больше действующего значения фазного тока и UЛ = UФ; IЛ = 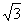IФ. При равномерной нагрузке фаз расчет трехфазной цепи соединенной треугольником, можно свести к расчету одной фазы. Фазное напряжение UФ = UЛ. Фазный ток IФ = UФ / ZФ, линейный ток IЛ = 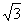IФ, угол сдвига по фазе φ = arctg (XФ / RФ).
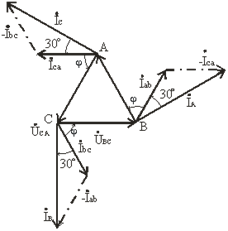Рис. 3.14