Что представляет собой угловая частота wсв в случае колебательного характера переходного процесса? Как она определяется расчётным путём и по осциллограмме?

Ответ: Как отмечалось в предыдущей лекции, линейная цепь охвачена единым переходным процессом. Поэтому в рассматриваемых цепях с одним накопителем энергии (катушкой индуктивности или конденсатором) – цепях первого порядка – постоянная времени будет одной и той же для всех свободных составляющих напряжений и токов ветвей схемы, параметры которых входят в характеристическое уравнение. Общий подход к расчету переходных процессов в таких цепях основан на применении теоремы об активном двухполюснике: ветвь, содержащую накопитель, выделяют из цепи, а оставшуюся часть схемы рассматривают как активный двухполюсник А (эквивалентный генератор) (см. рис.1, а) со схемой замещения на рис. 1, б.

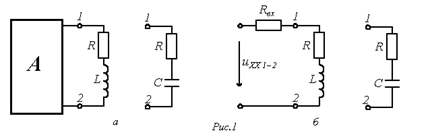
Совершенно очевидно, что постоянная времени здесь для цепей с индуктивным элементом определяется, как: 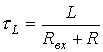, и с емкостным, как: 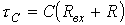, где 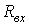- входное сопротивление цепи по отношению к зажимам 1-2 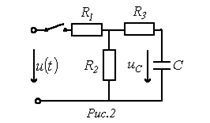подключения ветви, содержащей накопитель энергии. Например, для напряжения на конденсаторе в цепи на рис. 2 можно записать:

,

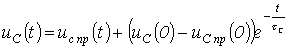где в соответствии с вышесказанным:

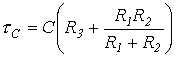. Переходные процессы при подключении последовательной
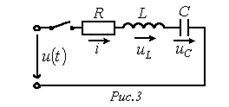R-L-C-цепи к источнику напряжения:

Рассмотрим два случая: а) 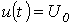; б) 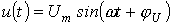. Согласно изложенной в предыдущей лекции методике расчета переходных процессов классическим методом для напряжения на конденсаторе в цепи на рис. 3 можно записать

.

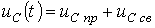(1)

Тогда для первого случая принужденная составляющая этого напряжения:

.

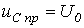(2)

Характеристическое уравнение цепи:

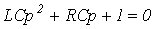, решая которое, получаем: .

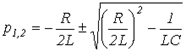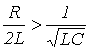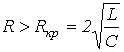В зависимости от соотношения параметров цепи возможны три типа корней и соответственно три варианта выражения для свободной составляющей: 1. или , где 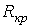- критическое сопротивление контура, меньше которого свободный процесс носит колебательный характер. В этом случае:

.

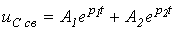(3)

2. 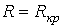- предельный случай апериодического режима. В этом случае 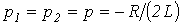и

.

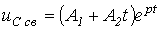(4)

3. 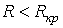- периодический (колебательный) характер переходного процесса.

В этом случае 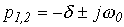и

,

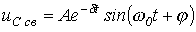(5)

где 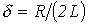- коэффициент затухания; 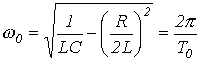- угловая частота собственных колебаний; 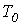- период собственных колебаний. Для апериодического характера переходного процесса после подстановки (2) и (3) в соотношение (1) можно записать:

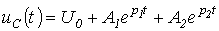. Для нахождения постоянных интегрирования, учитывая, что в общем случае 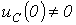и в соответствии с первым законом коммутации 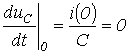, запишем для t=0 два уравнения: 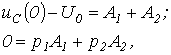решая которые, получим: 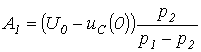; 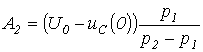. Таким образом,

. Тогда ток в цепи:

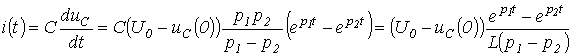
и напряжение на катушке индуктивности:

.

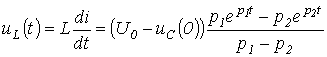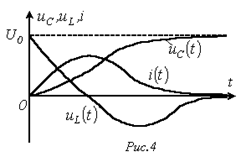На рис. 4 представлены качественные кривые 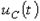, 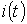и 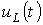, соответствующие апериодическому переходному процессу при 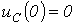. Для критического режима на основании (2) и (4) можно записать:

.

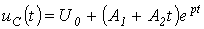При 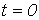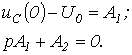Таким образом: 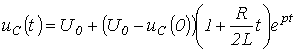и

.

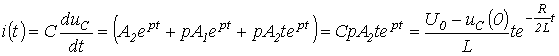Для колебательного переходного процесса в соответствии с (2) и (5) имеем: . Для нахождения постоянных интегрирования запишем 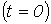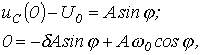откуда 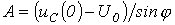и 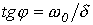. Тогда

.

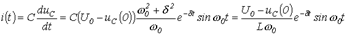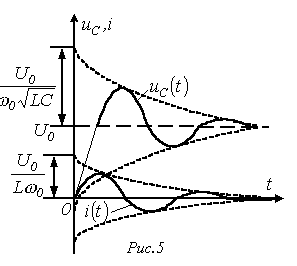На рис. 5представлены качественные кривые 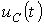и 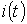, соответствующие колебательному переходному процессу при 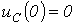. При подключении R-L-C-цепи к источнику синусоидального напряжения для нахождения принужденных составляющих тока в цепи и напряжения на конденсаторе следует воспользоваться символическим методом расчета, в соответствии с которым:

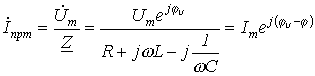
И 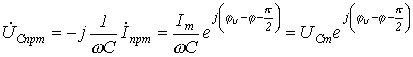, где ; ; .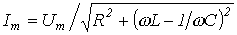

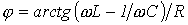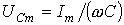Таким образом, 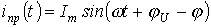и 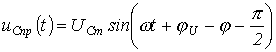. Здесь также возможны три режима:

1. 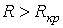;	2.	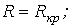3.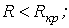

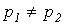
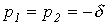
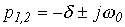
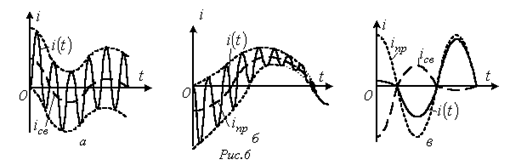
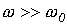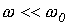Наибольший интерес представляет третий режим, связанный с появлением во время переходного процесса собственных колебаний с частотой . При этом возможны, в зависимости от соотношения частот собственных колебаний и напряжения источника, три характерные варианта: 1 - ; 2 - ; 3 - 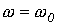, - которые представлены на рис. 6, а…6, в соответственно.