С бесконечными пределами интегрирования.

Лекция № 3-4.

Несобственные интегралы.

Мы рассматривали интегралы от функций, интегрируемых (и, следовательно, ограниченных) на конечных отрезках интегрирования. На практике возникает необходимость обобщения этих понятий на случаи, когда один из концов (или оба) отрезка интегрирования удален в бесконечность, либо функция не ограничена на отрезке интегрирования.

Несобственные интегралы от ограниченных функций

с бесконечными пределами интегрирования.

Иногда такой несобственный интеграл еще называют несобственным интегралом первого рода. В общем виде несобственный интеграл с бесконечным пределом чаще всего выглядит так: 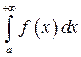. В чем его отличие от определенного интеграла? В верхнем пределе. Он бесконечный: .

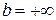Реже встречаются интегралы с бесконечным нижним пределом или с двумя бесконечными пределами: .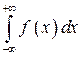

Использование несобственных интегралов, позволяет придать смысл такому понятию, как площадь полубесконечной (бесконечной) фигуры.

Изобразим на чертеже график подынтегральной функции 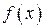. Типовой график и криволинейная трапеция для случая 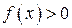выглядит так:

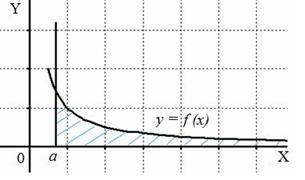
Несобственный интеграл 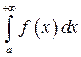численно равен площади заштрихованной фигуры, при этом возможны два случая:

1. Раз фигура бесконечная, то 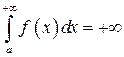, иными словами, площадь тоже бесконечна. Так быть может. В этом случае говорят, что несобственный интеграл расходится.

2. Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться конечному числу! Например: . Может ли так быть? Запросто. Во втором случае несобственный интеграл сходится.

В каких случаях несобственный интеграл расходится, а в каких сходится? Это зависит от подынтегральной функции .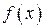

А что будет, если бесконечная криволинейная трапеция расположена ниже оси абсцисс? В этом случае, несобственный интеграл 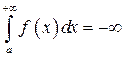(расходится) либо равен конечному отрицательному числу.

Мы рассматривали знакопостоянную функцию 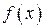для простоты интерпретации. На самом деле, подынтегральная функция может быть знакопеременной.

Определение 1. Пусть на интервале 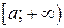задана функция 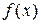, интегрируемая (следовательно, ограниченная) на любом отрезк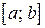е , где 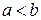. Тогда если существует , то он называется несобственным интегралом и обозначается .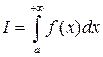

Аналогично определяются:

,

.

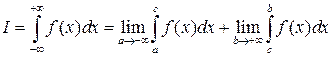В последнем случае предполагается, что 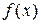интегрируема на любом отрезке; точку 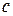можно выбрать произвольно.

В чем отличие неопределенного интеграла от определенного? Да ни в чем особенном! Как и в определенном интеграле, нужно уметь находить первообразную функцию 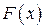(неопределенный интеграл), уметь применять формулу Ньютона-Лейбница. Единственное, что добавилось – это вычисление предела.

Пример 1. Исследовать на сходимость интеграл .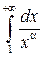

Решение. .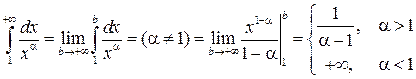

При 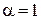имеем .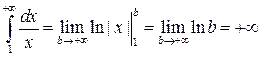

Таким образом, 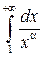сходится при 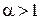и расходится при .

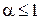Геометрический смысл этого результата состоит в том, что среди всех кривых вида 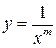гипербола 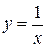является своеобразным «порогом»: те кривые данного вида, которые на полуинтервале 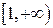лежат ниже неё, ограничивают полубесконечную фигуру конечной площади; если же кривая лежит выше или совпадает с гиперболой 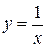, то соответствующая фигура имеет бесконечную площадь.

Пример 2. Вычислить несобственный интеграл 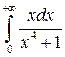или установить его расходимость.