
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Признаки сходимости для знакопеременных функций.
|
|
Формулировки приводятся для интегралов вида 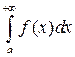 , но легко распространяются и на несобственные интегралы других типов.
, но легко распространяются и на несобственные интегралы других типов.
Определение 3. Несобственный интеграл 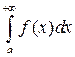 называется абсолютно сходящимся, если сходится интеграл
называется абсолютно сходящимся, если сходится интеграл 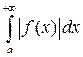 .
.
Определение 4. Если интеграл 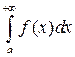 сходится, а интеграл
сходится, а интеграл 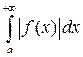 – расходится, то интеграл
– расходится, то интеграл 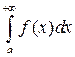 называется условно сходящимся.
называется условно сходящимся.
Теорема. Если 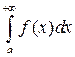 сходится абсолютно, то он сходится.
сходится абсолютно, то он сходится.
Признак Дирихле. Несобственный интеграл 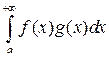 сходится, если выполняются следующие условия:
сходится, если выполняются следующие условия:
1) функция 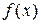 дифференцируема и монотонно стремится к нулю с ростом
дифференцируема и монотонно стремится к нулю с ростом 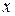 ;
;
2) функция  непрерывна и имеет ограниченную первообразную.
непрерывна и имеет ограниченную первообразную.
Примеры функций с ограниченной первообразной: 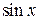 ,
, 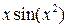 ,
, 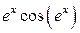 .
.
Признак Абеля. Несобственный интеграл 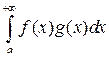 сходится, если выполняются следующие условия:
сходится, если выполняются следующие условия:
1) функция 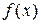 непрерывна на
непрерывна на 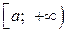 и
и 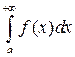 сходится;
сходится;
2) функция  ограничена, непрерывно дифференцируема и монотонна на
ограничена, непрерывно дифференцируема и монотонна на 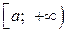 .
.
Утверждение. Если сходится интеграл 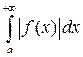 , то абсолютно сходятся интегралы
, то абсолютно сходятся интегралы 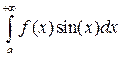 и
и  .
.
Пример 7. Интеграл Френеля 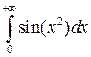 сходится, так как
сходится, так как
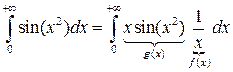 .
.
Пример 8. Интеграл Дирихле 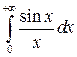 сходится условно.
сходится условно.
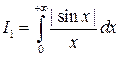 – расходится, так как
– расходится, так как 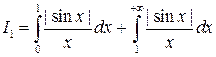 . Первый интеграл суммы сходится. Рассмотрим второй интеграл:
. Первый интеграл суммы сходится. Рассмотрим второй интеграл:
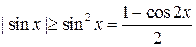 ,
,
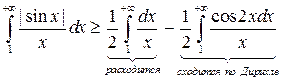 .
.
Интеграл 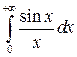 – сходится по признаку Дирихле:
– сходится по признаку Дирихле:
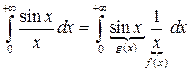 .
.