Решение уравнения при нелинейно-изменяющемся динамическом моменте и при изменяющемся моменте сопротивления

Математической основой является решение по методу последовательного приближения в соответствии с принципом конечных приращений. Применительно к классическому уравнению движения (1), этот принцип заключается в том, что бесконечно малые приращения угловой скорости 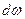и времени 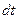заменяются соответственно малыми конечными приращениям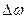и и , и .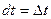

Точность решения задачи определяется величиной этих малых конечных приращений (интервала интегрирования) и выбирается исходя из оптимального соотношения точности и сложности:

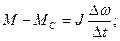(95)

.

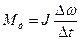На основании (13) составляется пропорция:

(96)

Существует 2 вида решения задач:

1) графическое;

2) графоаналитическое.

1) Графический метод называется методом пропорций.

Последовательность графического решения:

1. В декартовой системе координат во 2-ом квадранте координатной плоскости, строится в масштабе механические характеристики двигателя: и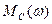

ЭП: АД- турбомеханизму

Рис.74. Графическое решение задачи.

2. Построим совместную механическую характеристику ЭП: арифметическую разность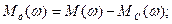

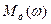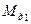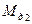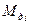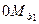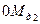
3. Разбиваем кривую на участки с , , …, с помощью циркуля проецируем отрезки , , 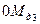…, 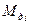на ось ординат.

4. Откладываем вдоль оси абсцисс в масштабе отрезок ОА, который равен в выбранном масштабе .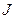

По теореме о подобии :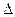

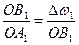
В этом выражении левая часть пропорциональна:

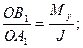для определения масштаба времени, используем пропорцию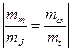

Если из начала координат повести отрезок 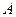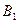до пересечения с ординатой 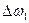, то проекция этого отрезка на ось абсцисс будет соответствовать величине 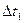. Если из конца того отрезка провести прямую параллельную до пересечения с , то 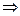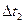. Таким образом, построив отрезки прямых, параллельных лучам, проведённым из 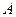т. в т. 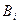до величины установившейся угловой скорости получим ломанную кривую, состоящую из отрезков прямых - кривую разгона.

Рассмотренный метод носит название: метод пропорций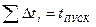

2) Более точным, универсальным и удобный является – графоаналитический метод расчета (метод площадей).

Сущность метода, та же что и метода пропорций: замена 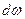и 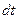на малые конечные 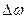и

После чего (13) имеет вид:

(97)

Если решить относительн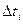о , то .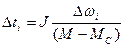

1. Во втором квадранте плоскости Декартовых координат в одном масштабе строятся:

- механическая характеристика двигателя ;

- механическая характеристика механизма .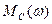

Рассмотрим тот же пример, что и по методу пропорций:

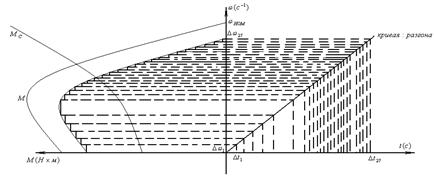
Рис.75. Решение задачи при графоаналитическом методе.

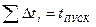
2. Строим совместную механическую характеристику ЭП:

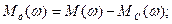
Кривую 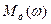по оси ординат разбиваем на ряд участков с шагом 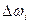, который на всём диапазоне принимается одинаковым.

При этом 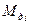на каждом участке интегрирования:

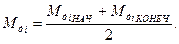
Тогда:

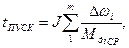(98)

где 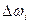- шаг разбиения по оси ординат;

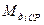- среднее значение 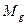на каждом участке разбиения.

Если мы для каждого участка разбиения найдём 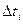, отложим эти значения вдоль оси абсцисс в 1-ом квадранте в масштабе времени, а затем проведём отрезки до пересечения с ,

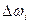то получим кривую разгона двигателя в пределе на интервале интегрирования равную .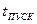

Последовательность операций определения 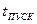по методу площадей сведём в таблицу.

№ участка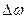
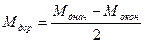
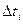
. . . n	. .	. . . . . . .	. . . . . . .	. . . . . . .	. . . . . . .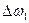

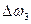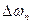
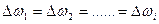
Поставим перед собой задачи:

а) Рассчитать длительность процесса самоторможения, используя метод площадей.

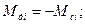
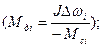
Последовательность такой задачи будет отличаться от предыдущей тем, что интегрироваться будет 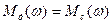. Поэтому, интегрируя кривую 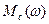в той же последовательности, что и в предыдущей задаче, определим время самоторможения.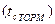

б) определим время электрического торможения, например динамического, имея в виду, что функция определена экспериментально или рассчитана. Можно определить по формуле Клосса, только необходимо знать , .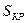

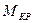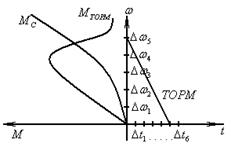
Рис. 76 Механические характеристики при электрическом торможении.