Понятие математической модели, свойства и классификация

Модель – это физический или абстрактный образ моделируемого объекта, удобный для проведения исследований и позволяющий адекватно отображать интересующие исследователя физические свойства и характеристики объекта.

Математическая модель – это совокупность математических объектов и отношений между ними, адекватно отображающая физические свойства технического объекта.

На различных этапах и стадиях проектирования сложной технической системы используют различные математические модели. Математические модели могут представлять собой системы дифференциальных уравнений, системы алгебраических уравнений, простые алгебраические выражения, бинарные отношения, матрицы и так далее. Уравнение математической модели связывают физические величины.

К математическим моделям предъявляются требования адекватности, экономичности, универсальности. Модель считается адекватной, если отражаются исследуемые свойства с приемлемой точностью.

Математические модели технических объектов, используемые при проектировании, предназначены для анализа процессов функционирования объектов и оценки их выходных параметров. Они должны отражать физические свойства объектов, существенные для решения конкретных задач проектирования. При этом математическая модель должна быть как можно проще, но в то же время обеспечивать адекватное описание анализируемого процесса.

Используют следующие виды математических моделей: детерминированные и вероятностные, теоретические и экспериментальные факторные, линейные и не линейные, динамические и статистические, непрерывные и дискретные, функциональные и структурные.

По форме представления математических моделей различают:

1. Инвариантная модель – математическая модель, представляющаяся системой уравнений (дифференциальных, алгебраических), вне свези с методом решения этих уравнений.

2. Алгебраическая модель – соотношение моделей связаны с выбранным численным методом решения и записаны в виде алгоритма (последовательности вычислений).

3. Аналитическая модель – представляет собой явные зависимости искомых переменных от заданных величи н.

Такие модели получают на основе физических законов, либо в результате прямого интегрирования исходных дифференциальных уравнений, используя табличные

интегралы. К ним относятся также регрессионные модели, получаемые на основе результатов эксперимента.

4. Графическая модель – представляется в виде графиков, эквивалентных схем, динамических моделей, диаграмм и тому подобное. Для использования графических моделей должно существовать правило однозначного соответствия условных изображений элементов графической и компонентов инвариантной математической модели.

Математические модели могут представлять собой функциональные зависимости между выходными, внутренними и внешними параметрами.

Деление математических моделей на функциональные и структурные определяется характером отображаемых свойств технического объекта.

Структурные модели отображают только структуру объектов и используются при решении задач структурного синтеза. Параметрами структурных моделей являются признаки функциональных или конструктивных элементов, из которых состоит технический объект и по которым один вариант структуры объекта отличается от другого. Такие модели имеют форму таблиц, матриц и графиков. Они наиболее широко используются на метоуровне при выборе технического объекта.

Функциональные модели описывают процессы функционирования технических объектов и имеют форму систем уравнений. Их широко используют на всех иерархических уровнях, стадиях и этапах при функциональном, конструкторском и технологическом проектировании.

По способам получения функциональные математические модели делятся на:

1.Теоретические модели – получают на основе описания физических процессов функционирования объекта.

2. Экспериментальные модели – получают на основе поведения объекта во внешней среде, рассматривая его как кибернетический " черный ящик".

При построении теоретических моделей используют физический и формальный подходы. Физический подход сводится к непосредственному применению физических законов для описания объектов. Формальный подход используется при построении как теоретические, так и экспериментальные модели.

Функциональные математические модели могут быть:

1. Линейные модели, содержащие только линейные функции фазовых переменных и их производных.

2. Нелинейные математические модели, включающие в себя нелинейные функции фазовых переменных и их производных.

Если при моделировании учитывается инерциальные свойства технического объекта и (или) изменение во времени параметров объекта или внешней среды, то модель называют динамической. В противном случае модель статическая. Выбор динамической или статической модели определяется режимом работы технического объекта.

Математическое представление динамической модели в общем случаи может быть выражено системой дифференциальных уравнений, а статической – системой алгебраических уравнений. Динамическая модель может также представлять собой интегральные уравнения, придаточные функции, а в аналитической форме – явные зависимости фазовых координат или выходных параметров технического объекта от времени.

1.2 Численные методы в математическом моделировании

Любой численный метод линейной алгебры можно рассматривать как некоторую последовательность выполнения арифметических операций над элементами входных данных. Если при любых входных данных численный метод позволяет найти решение задачи за конечное число арифметических операций, то такой метод называется прямым. В противоположном случае численный метод называется итерационным. Прямые методы - это такие, как метод Гаусса, метод окаймления, метод пополнения, метод сопряжённых градиентов и др. Итерационные методы – это метод простой итерации, метод половинного деления, метод переменных направлений, метод простых итераций метод хорд и др.

На практике в большинстве случаев найти точное решение возникшей математической задачи не удается. Это происходит главным образом не потому, что мы не умеем этого сделать, а поскольку искомое решение обычно не выражается в привычных для нас элементарных или других известных функциях. Поэтому важное значение приобрели численные методы, особенно в связи с возрастанием роли математических методов в различных областях науки и техники и с появлением высокопроизводительных ЭВМ.

Под численными методами подразумеваются методы решения задач, сводящиеся к арифметическим и некоторым логическим действиям над числами, т.е. к тем действиям, которые выполняет ЭВМ.

Для того чтобы понять суть решения уравнений на ЭВМ необходимо обладать некоторыми теоретическими навыками такими как:

а) последовательность решения.

б) теоремами и формулами решения.

Численное решение нелинейных (алгебраических или трансцендентных)

уравнений вида:

f(x)=0 (1.1.1)

Заключается в нахождении значений x, удовлетворяющих (с заданной точностью) данному уравнению и состоит из следующих основных этапов:

а) Отделение (изоляция, локализация) корней уравнения.

б). Уточнение с помощью некоторого алгоритма конкретного выделенного корня с заданной точностью.

Целью первого этапа является нахождение отрезков из области определения

функции, внутри которых содержится только один корень решаемого. Иногда ограничиваются рассмотрением лишь какой-нибудь части области определения, вызывающей по тем или иным соображениям интерес. Для реализации данного этапа используются графические или аналитические способы.

При аналитическом способе отделения корней полезна следующая теорема:

Непрерывная строго монотонная функция f(x) имеет и притом единственный нуль на отрезке [a, b] тогда и только тогда, когда на его концах она принимает значения разных знаков.

При завершении первого этапа, должны быть определены промежутки, на каждом из которых содержится только один корень уравнения. На втором этапе нам необходимо уточнить на каком участке находятся корни, с помощью теоремы:

Пусть на отрезке [a, b] функция имеет первую и вторую производные постоянного знака и пусть f(x) f (a)f (b) < 0. Тогда если точка 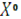выбрана на [a, b] так, что:

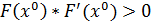(1.1.2)

Метод хорд

Первым, кто смог найти приближенные решения кубических уравнений, был Диофант, тем самым заложив основу метода хорд. Сохранившиеся работы Диофанта сообщают об этом. Однако первым, кто понял его методы, был Ферма в XVII веке, а первым, кто дал объяснение методу хорд, был Ньютон(1670-е гг.).

Метод хорд — итерационный метод нахождения корня уравнения. Суть метода состоит в разбиении начального отрезка на части, определяемые с помощью точки пересечения хорды – отрезка, соединяющего точки, соответствующие значениям функции на концах отрезка, с осью Ох.

Геометрическое описание

Будем искать корень функции f(x). Выберем две начальные точки C ₁(x ₁; y ₁) и C ₂(x ₂; y ₂) и проведем через них прямую. Она пересечет ось абсцисс в точке (x ₃; 0). Теперь найдем значение функции с абсциссой x ₃. Временно будем считать x ₃ корнем на отрезке [ x ₁; x ₂]. Пусть точка C ₃ имеет абсциссу x ₃ и лежит на графике. Теперь вместо точек C ₁ и C ₂ мы возьмём точку C ₃ и точку C ₂. Теперь с этими двумя точками проделаем ту же операцию и так далее, т.е. будем получать две точки C_{n + 1} и C_n и повторять операцию с ними. Таким образом мы будем получать две точки, отрезок, соединяющий которые, пересекает ось абсцисс в точке, значение абсциссы которой можно приближенно считать корнем. Эти действия нужно повторять до тех пор, пока мы не получим значение корня с нужным нам приближение

Алгебраическое описание метода

Пусть x ₁, x ₂ − абсциссы концов хорды, y = kx + b − уравнение прямой, содержащей хорду. Найдем коэффициенты k и b из системы уравнений:

(1.2.1)

Вычтем из первого уравнения второе: f (x ₁) − f (x ₂) = k (x ₁ − x ₂), затем найдем коэффициенты k и b:

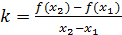(1.2.2)

Тогда 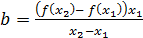(1.2.3)

Уравнение принимает вид:

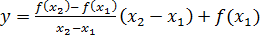(1.2.4)

Таким образом, теперь можем найти первое приближение к корню, полученное методом хорд:

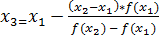(1.2.5)

Теперь возьмем координаты x2 и x3 и повторим все проделанные операции, найдя новое приближение к корню. Повторять операцию следует до тех пор, пока

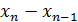| | не станет меньше или равно заданному значению погрешности.

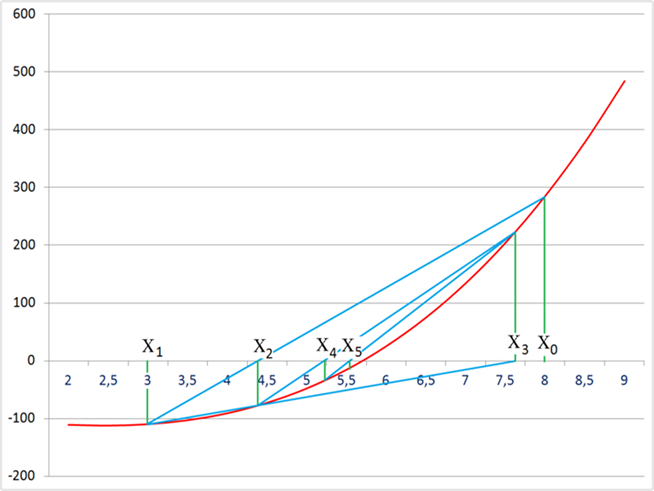
Рисунок 1.2.1 Пример расчета на графике методом хорд.