Описание исследований
Опыты заключаются в том, что используя начальные исходные данные, но изменяя в каждом последующем опыте внутренний радиус, решаем изменённое дифференциальное уравнение с помощью функции root.
| -нумерация элементов заданных векторов будет начинаться с 1
| | Выбираем переменную jо т 1 д о 7
| | j- номер опыта и номер элемента в векторе R1
|
| Исследуем значения варьируемого параметра по преобразованной формуле:
| | - начальное приближенное значение корня
| | Применяем функцию root для нахождения корней
|
Полученные корни внешнего радиуса R2 при варьируемых значениях внутреннего радиуса R1
Таким образом проделали 7 опытов благодаря функции root. Все расчеты приведены в приложении Б так же строим графики зависимости рисунок Б.1 и Б.2 показанный в расчетах.
Итогом данной курсовой работы является построение графика аналитической аппроксимирующей зависимости R2k от значений коэффициента внутреннего радиуса.
| Задаем вектор функции линейной регрессии общего вида:
| | Задаем полученную функцию линейной регрессии общего вида
| | - коэффициенты подобранной регрессионной зависимости
|
| а п п р о к с и м у р и у ю щ а я ф у н к ц и я
| | Э к с п е р е м е н т а л ь н ы е д а н н ы е
|
 Рисунок 3.2.1 График аппроксимирующей функции Рисунок 3.2.1 График аппроксимирующей функции
Линейная регрессия общего вида реализуется с помощью функции linfit:
linfit(R1, R2k, Z),
где
R1, R2k – координаты исходных точек;
Z - вектор, содержащий функции F(x), записанные в символьном виде.
Функция linfit еще называется функцией аппроксимации по методу наименьших квадратов.
|


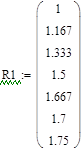

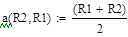
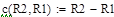
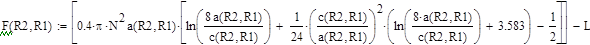
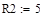
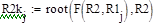
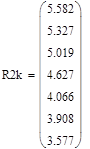

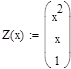
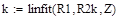
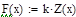
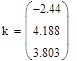
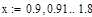
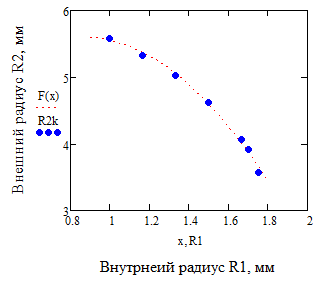


 Рисунок 3.2.1 График аппроксимирующей функции
Рисунок 3.2.1 График аппроксимирующей функции