Исследование колебаний подпрыгивания пути и ж. д. экипажа с одноступенчатым рессорным подвешиванием.

Составим уравнения колебаний для модели рельсового экипажа в виде механической системы, включающей в себя две массы: масса 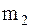, моделирующая кузов и масса 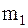, моделирующая тележку. Эти массы связаны между собой через кузовную подвеску, состоящую из пружины жесткостью 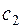и гасителя колебаний с коэффициентом демпфирования 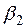(рис.1). Экипаж движется по деформируемому пути с неровностью 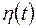. Будем считать, что инерционные, упругие и диссипативные свойства пути можно моделировать сосредоточенной массой 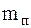(приведенная масса части верхнего строения пути) перемещающейся вертикально вместе с колеблющейся колесной парой и прикрепленной к основанию с помощью вязкоупругой связи с параметрам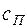и и 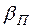. Предполагаем, что по горизонтали система перемещается с постоянной скоростью .

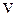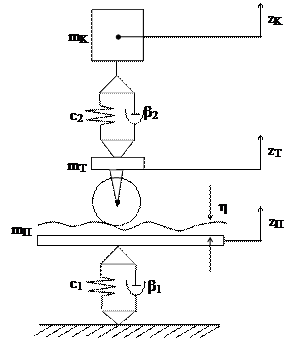
Рисунок 1 – Расчетная схема для исследования колебаний подпрыгивания пути и железнодорожного экипажа с одинарным рессорным подвешиванием

Рисунок 2 – Расчетная схема четырехосного вагона с одинарным рессорным подвешиванием

Из сравнения расчетных схем на рисунке 1 и рисунке 2 легко видеть, что , , , .

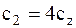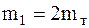Рассматриваемая система имеет две степени свободы. За обобщенные координаты примем отсчитываемые от равновесного положения и определяющие положение центров масс тележки и кузова. При условии безотрывного качения колеса по рельсу перемещение точки пути под колесом .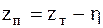

Уравнения Лагранжа второго рода для рассматриваемой системы запишем в виде

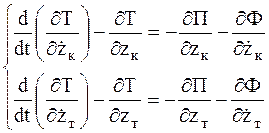(5.1)

Кинетическая энергия системы может быть представлена в виде:

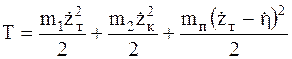(5.2)

Потенциальная энергия сил тяжести запишется как

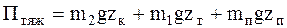(5.3)

Потенциальная энергия сил упругости имеет вид

(5.4)

Деформация пружины моделирующей упругость пути 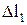находится как

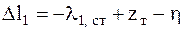
где 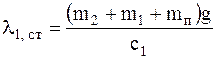– статическая деформация пружины 1.

Деформация пружины 2

.

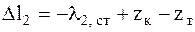Статическая деформация пружины 2

.

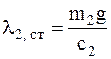Окончательно выражение потенциальной энергии системы принимает вид:

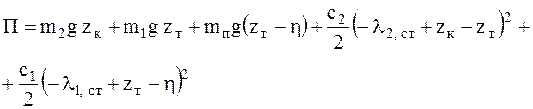. (5.5)

Частные производные от потенциальной энергии по обобщенным координатам равны

,

.

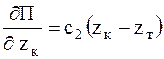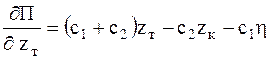Диссипативная функция Рэлея в данном случае имеет вид

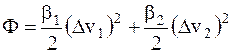, (5.6)

где – разность скоростей верхней и нижней точек крепления демпфера 1,

и соответственно

.

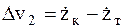Окончательно выражение диссипативной функции принимает вид

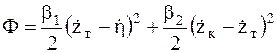. (5.7)

Частные производные от диссипативной функции Рэлея по обобщенным скоростям равны:

,

.

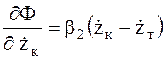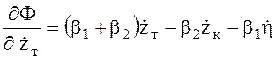С учетом выражений (5.5) и (5.7) уравнения Лагранжа второго рода рассматриваемой системы будут иметь вид

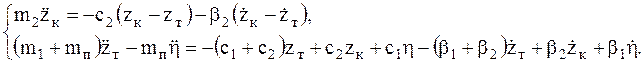
Перенося члены, содержащие неизвестные из правой части в левую, получим

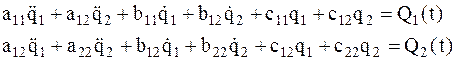(5.8)

Таким образом, для нашей системы

, , ,

, , ,

, , .

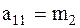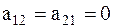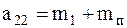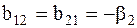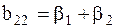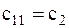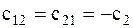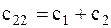Парциальные частоты 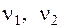для рассматриваемой системы будут равны

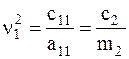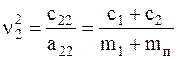; . (5.9)

Для железнодорожных экипажей обычно 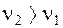, так как 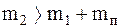. Для определения собственных частот колебаний экипажа составим частотное уравнение

.

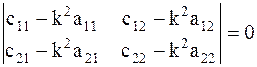В нашем случае частотное уравнение имеет вид

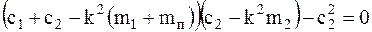
или

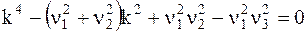, (5.10)

где .

. (5.11)

В соответствии с тем, что 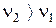, из формулы видно, что 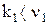, 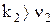. Меньшую из частот 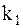называют основной частотой.

Рассмотрим собственные колебания этой системы при отсутствии сил вязкого сопротивления гасителей. Положим 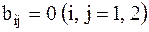, а правые части уравнений (5.8) приравняем нулю

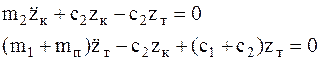(5.12)

Частными решениями однородной системы (5.12) будут

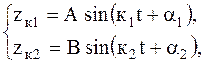
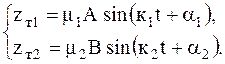(5.13)

Колебания совершаемые системой с одной из собственных частот 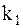или 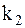называются главными колебаниями. Главное колебание соответствующее меньшей собственной частоте 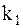называют основным колебанием, так как это колебание является основным в результирующем движении системы.

Коэффициенты 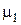и

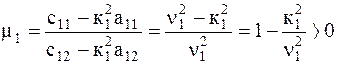, (5.14)

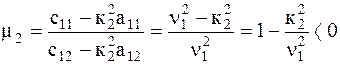(5.15)

называют коэффициентами распределения амплитуд. Они характеризуют отношение амплитуд в главных колебаниях или форму главных колебаний (коэффициент формы).

Из (5.14–5.15) следует, что в первом главном виде колебаний системы 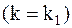перемещения всегда совпадают по знаку, т. е. обе массы со­вершают колебание в одной фазе, а во втором главном виде 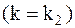– в противофазах (навстречу друг другу).

В общем случае собственные колебания кузова и тележек вагона определяются зависимостями:

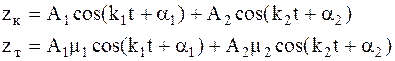(5.16)

где амплитуды 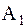, 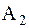и начальные фазы 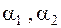определяются из на­чальных условий. Периоды (в секундах) колебаний основного (с на­именьшей частотой 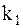) тона Т₁ и наложенного Т₂ определяются из выражений

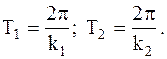
Частоты колебаний 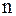выражены числом колебаний в секунду (Гц) в отличие от угловых частот (рад/с):

(5.17)

Для современного груженого четырехосного вагона и пути с деревянными шпалами имеем:

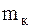= 80 т; 2 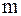_т = 14 т; 4 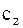= = 16 МН/м; 8 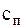= 400 МН/м. Парциальные частоты 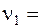14, 1 с^-1, 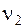= 172 с^-1;

главные частоты 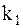= 13, 8 с^-1 (2, 2 Гц), 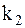= 172 с^-1 (27 Гц).

Следовательно, частота второго вида колебаний 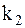более чем на порядок выше частоты 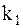первого вида.

Собственные колебания масс кузова и тележки (см. рис.3), представляющие собой сумму двух гармонических колебаний, являются незатухающими, так как при решении задачи мы пренебрегли действием неупругих сил сопротивления гасителей, которые служат для гашения собственных колебаний.

Вынужденные колебания масс рассматриваемой системы характеризует система дифференциальных уравнений (5.8) при условии, что 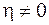. Как и ранее, будем пренебрегать силами сопротивления гасителей ()

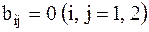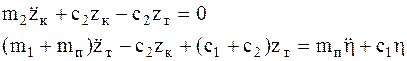(5.18)

Для упрощения вычислений положим, что неровность рельсовых нитей может быть выражена как

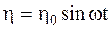(5.19)

где 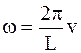– частота чередования неровностей пути с длиной волны L при движении вагона со скоростью .

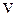Такое допущение целесообразно, хотя бы потому, что любая сложная непрерывная вертикальная неровность пути может быть представ­лена рядом, состоящим из суммы гармонических функций с различ­ными амплитудами и периодами. Так как исследование системы часто сводится к линейным дифференциальным уравнениям, то решение их для сложной функции возмущения (неровности) можно получить как сумму решений для ее гармонических составляющих.

Частное решение системы дифференциальных уравнений (5.18) следует искать в виде гармонических функций, сходных с функциями возмущения

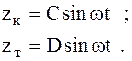(5.20)

Подставив выражения (5.20) в уравнения (5.18) и приравнивая коэффициенты при синусах, получим

.

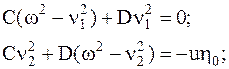
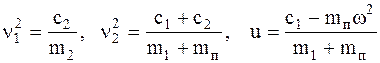Из последних выражений найдем

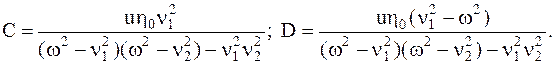(5.21)

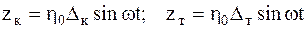(5.22)

где 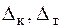–коэффициенты нарастания амплитуд (коэффициенты динамичности)

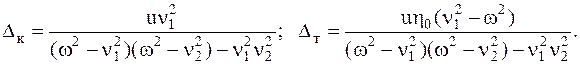
Полное решение системы уравнений (5.8) с правой частью получим суммированием общих решений (5.16) для однородной системы с по­лученным частным решением (5.22) для неоднородной системы.

Учитывая, что собственные колебания исследуемой системы затух­нут при условии, когда движение по пути с непрерывной неровностью будет длительным, практический интерес представляет изучение только вынужденных колебаний системы, характеризуемый выражениями (5.22). Амплитуды этих колебани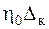й и 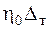изменяются по закону изменения коэффициентов нарастания 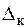, 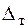в зависимости от частоты 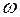или от скорости .

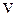При весьма малых скоростях и больших длинах волн неровностей величина 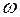мала по сравнению с и 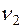. Тогда из уравнения (5.21) с учетом выражения (5.9) получим

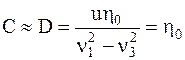(5.23)

Следовательно, обе массы колеблются с амплитудой неровности пу­ти без деформации связей (рессор и подрельсового основания).

Сравнивая знаменатели выражений (5.21) с частотным уравнением (5.10), нетрудно видеть, что значения С и D будут весьма большими при 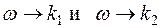. Значит, существуют две резонансные частоты 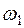и 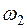и соответственно две критические скорост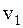и и 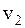, при которых амплитуды вынужденных колебаний масс 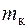и 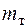неограниченно увеличиваются.

Отношение амплитуд колебаний тележек и кузова вагона будет

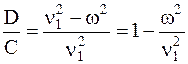. (5.24)

Из выражения (5.24) видно, что при скоростях движения, для которых 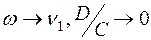, т. е. величина D мала по сравнению с величиной С.

Для грузовых вагонов в груженом состоянии это будет иметь место при движении с эксплуатационными скоростями 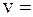20÷ 25 м/с по пути с длиной волн неровностей

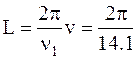(20÷ 25) = 9÷ 11 м.

Такие неровности относятся к разряду длинных. Если неровности будут короткими (в 5—10 раз короче указанных), то при тех же скоростях движения величина D по абсолютному значению будет во много раз превосходить величину С и перемещения будут иметь обратные знаки. Следовательно, при изучении колебаний кузова (например, для оценки плавности хода загруженного вагона) необходимо рассматривать движение по пути с длинными неровностями, пренебрегая влиянием относительно коротких. При этом в расчетной схеме допускается не учитывать наличие неподрессоренных масс тележек и приведенных масс верхнего строения пути, а ограничиться рассмотрением колебаний кузова на рессорах. И, наоборот, при исследовании динамики неподрессоренных масс вагона необходимо рассматривать его движение по коротким неровностям, а колебания подрессоренной массы кузова в расчетной схеме не учитывать, так как они практически не влияют на процесс колебания неподрессоренных частей.