Слабого электролита

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Способность раствора электролита проводить электрический ток обусловлена движением ионов, которые образуются вследствие электролитической диссоциации вещества. Для характеристики способности электролита проводить электрический ток или электропроводимости используют величины удельной χ и мольной λ электропроводностей, которые могут быть представлены выражениями:

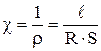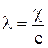, , (1)

где ρ – удельное сопротивление электролита, Ом·м;

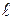– толщина слоя электролита, через который протекает электрический ток, м;

S – площадь поперечного сечения слоя электролита, м²;

R – электрическое сопротивление слоя электролита, Ом;

с – концентрация электролита, моль/м³.

Из выражений (1) следует, что удельная электропроводность χ имеет размерность Ом^-1·м^-1 или См/м; а мольная электропроводность λ – Ом^-1·м² ·моль^-1 или См·м²/моль.

Согласно закону Ома i = – χ grad φ, где i – плотность тока, А/м²; φ – электрический потенциал, В; grad – оператор градиента, 1/м, удельная электропроводность численно равна силе токе (А), проходящей через слой раствора с поперечным сечением 1м² под действием градиента потенциала 1 В/м.

Понятие удельной электропроводности чаще используют для целей электролиза, в то время как понятие мольной электропроводности более удобно при теоретическом анализе.

Мольная электропроводность равна проводимости слоя электролита толщиной 1м, помещенного между одинаковыми электродами такой площади, чтобы объем раствора, заключенный между ними, содержал 1 моль растворенного вещества. Таким образом, по мере разбавления раствора площадь контакта электродов с электролитом и объем электролита увеличиваются.

Мольная электропроводность зависит от концентрации раствора. С уменьшением концентрации она увеличивается и достигает предельного значения, которое называется электропроводностью при бесконечном разведении и обозначается 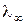или λ _о.

Для слабых электролитов зависимость мольной электропроводности от концентрации раствора определяется изменением степени диссоциации

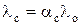, (2)

где a_с – степень диссоциации при концентрации электролита с; λ _с – мольная электропроводность при концентрации электролита равной с.

Мольная электропроводность любых электролитов выражается через молярные проводимости катиона и аниона

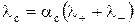, (3)

где λ ₊ и λ _- – молярные проводимости катиона и аниона соответственно, См·м²/моль.

Молярные проводимости ионов определяются произведением их ионной подвижности U и V на постоянную Фарадея:

λ ₊ = U₊·F, λ _- = V_–·F, (4)

где U₊ и V_– – ионные подвижности катиона и аниона соответственно, м²/В·с. Для сильных электролитов, для которых a = 1, справедливо уравнение

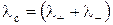. (5)

При бесконечном разведении, когда a 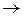1, уравнения (3) и (5) переходят в уравнение

λ _о = 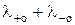, (6)

где λ _+о и λ _-о – молярные проводимости катиона и аниона при бесконечном разведении соответственно, См·м²/моль.

Мольная электропроводность сильных электролитов до концентраций не выше 0, 02 М описывается уравнением Кольрауша, которое позднее теоретически было обосновано Онзагером

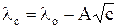. (7)

Постоянная А зависит от природы растворителя, температуры и валентного типа электролита.

Измерение электропроводности растворов слабых электролитов дает возможность определить константу электролитической диссоциации, связанную со степенью диссоциации уравнением

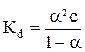. (8)

Подставив из уравнения (2) выражение степени диссоциации a_с= 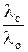в уравнение (8), получим

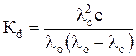. (9)

Решив уравнение (9) относительно произведения λ _с·с, после некоторых преобразований получим

λ _с·с = 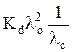– K_d λ _o, (10)

то есть произведение λ _с·с является линейной функцией 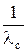, что можно записать в виде

λ _с·с = а 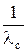+ b, (11)

где а = 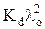, b = –K_d λ _o.

Из графика зависимости λ _с·с = f 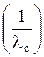можно найти значения величин а и b, используя которые рассчитать затем λ _o и К_d по уравнениям:

λ _o = 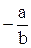, К_d = – (12)

Для слабых электролитов, степень диссоциации которых незначительна, что справедливо для растворов с концентрацией больше 0, 01, в знаменателе уравнения (8) можно пренебречь величиной a по сравнению с единицей, тогда

К_d 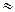a²c. (13)

Заменив теперь степень диссоциации отношением электропроводностей, получим:

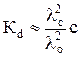. (14)

После логарифмирования уравнение (14) примет вид

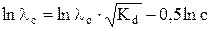. (15)

Если известна величина λ _o, то, построив график в координатах ln λ _c – ln c, можно рассчитать K_d слабого электролита.

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

Цель работы – установление K_d и λ _о бинарного слабого электролита.

В экспериментах определяют удельную электропроводность растворов электролита различных концентраций с применением моста переменного тока (рис.1) или кондуктометра, что позволяет устранить влияние поляризации электродов и тем самым повысить точность измерения.

Источник переменного тока представляет собой генератор синусоидального напряжения с частотой 600 – 5000 Гц. Детектором тока служит микроамперметр (Г) или осциллограф. В два плеча моста включены ячейка с раствором электролита R_x и регулируемые магазин соп­ротивлений R₂ и емкость С; два других плеча – стандарт­ные сопротивления R₁ и R₃.

Мост балансируется путем регулирования R₂ и С таким образом, чтобы гальванометр показал отсутствие тока в диагона­ли моста АВ. Отсутствие тока означает, что разность потенциалов между точками А и В равна нулю и падение напряжения на R₁ и R₃ равно падению напряжения на R₂ и R_x.

При этом выполняется соотношение:

(16)

Это условие баланса моста, из которого следует, что

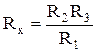. (17)

Балансировка моста переменного тока осложняется влиянием индуктив­ностей и ёмкостей катушек сопротивления и ёмкостей электролитической ячейки с раствором. Влияние индуктивности устраняют применением катушек с безиндуктивной намоткой. Для балансировки емкостей используют регулируемый конденсатор С. При измерениях следует добиваться четкого снижения сигнала детектора до нуля путем одновременной регулировки R₂ и С.

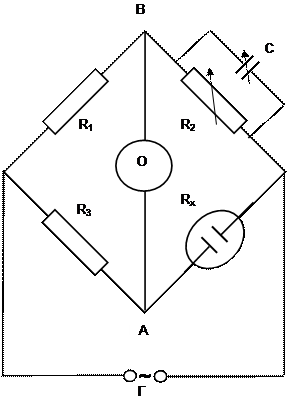Рис.1. Схема моста переменного тока.

О – осциллограф, Г – источник переменного тока

Чтобы по результатам измерений можно было рассчитать истинную удельную электропроводность, измерительную ячейку градуируют по стандартному раствору и рассчитывают постоянную ячейки по уравнению

R = 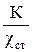, (18)

где К – постоянная ячейки; χ _ст – известная удельная электропроводность стандартного электролита.

В качестве стандартного раствора применяют водные растворы хлорида калия определенных концентраций, удельная электропроводность которых известна. В случае применения кондуктометра постоянную ячейки не определяют и стандартные растворы хлорида калия не требуются.

При использовании кондуктометра специальной конструкции возможно прямое измерение удельной электропроводности.

Порядок выполнения работы

1. Готовят стандартные растворы хлорида калия с концентрациями 0, 1 и 0, 01М.

2. Измеряют сопротивление воды, используемой для приготовления растворов.

3. Приготовленным раствором хлорида калия сначала ополаскивают, а затем заполняют измерительную ячейку, которую помещают в термостат на 20 – 30 минут.

4. Измеряют сопротивление растворов хлорида калия и по уравнению

(18) рассчитывают постоянную сосуда и удельную электропроводность воды.

Внимание. Объем раствора в ячейке должен быть постоянным во всех измерениях.

5. Готовят растворы слабого электролита с концентрациями в интервале от 0, 001 до 0, 02 М, значение которых задаёт преподаватель.

6. Измеряют электрическое сопротивление этих растворов R_раств и рассчитывают их удельную электропроводность χ _раств по формуле (18).

7. В случае применения кондуктометра необходимость в стандартных растворах хлорида калия отпадает.

χ _раств = . (19)

Обработка результатов опыта

1. Рассчитывают мольную электропроводность кислоты по уравнению

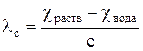, (20)

где χ _раств – удельная электропроводность раствора концентрации с, См/м;

χ _вода – удельная электропроводность воды, См/м;

с – концентрация раствора, моль/м³;

λ _с – мольная электропроводность раствора концентрации с, См·м²/моль;

2. Используя программу EXСEL или подобную ей, строят график в координатах λ _с·с = f 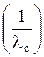, обрабатывают его уравнением прямой линии, используя метод наименьших квадратов, и по формулам (12) и (2) рассчитывают мольную электропроводность при бесконечном разведении, константу диссоциации и степень диссоциации.

Экспериментальные и рассчитанные результаты сводят в таблицы 1 и 2.

Таблица 1. Экспериментальные и расчетные результаты

Таблица 2. Экспериментальные и расчетные результаты

Концентрация раствора электролита с, моль/м3	Мольная электропроводность раствора электролита λ с, Cм·м2/моль	λ с·с, См/м		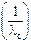Мольная электропроводность раствора электролита при бесконечном разведении λ о, См·м2/моль	Константа диссоциации Кd	Степень диссоциации a

По результатам работы делают выводы и вычисляют абсолютную и относительную ошибки.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Дать определение удельной и мольной (эквивалентной) электропроводностей. Как они связаны между собой? В каких единицах измеряются?

2. Какими величинами характеризуется процесс диссоциации? Чем отличаются сильные и слабые электролиты?

3. Как зависит удельная электропроводность от концентрации электролита?

4. Как зависит мольная (эквивалентная) электропроводность от концентрации электролита? Уравнение Кольрауша для сильных электролитов.

5. Написать уравнение связи между эквивалентной (молярной) электропроводностью и степенью диссоциации электролита.

6. Написать уравнение связи между константой диссоциации и степенью диссоциации для 1-1 валентного электролита.

7.Вывести уравнение, из которого графически, зная концентрацию электролита и мольную (эквивалентную) электропроводность, можно определить константу диссоциации. Показать расчет.

8. Зависимость удельной и эквивалентной электропроводности от температуры.

9. Какие физико-химические свойства растворов могут быть найдены благодаря измерению проводимости электролитов?

10.Запишите закон разбавления Оствальда через эквивалентную проводимость.

11. В чем сущность компенсационного метода измерения электропроводности?

12. Зависимость степени диссоциации и константы диссоциации от температуры.

13. Размерности величин в уравнениях.