
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение средней активности и среднего коэффициента активности соляной кислоты методом ЭДС
|
|
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
С термодинамической точки зрения в растворах любых электролитов (сильных или слабых) всегда существует равновесие
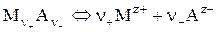 , (1)
, (1)
где 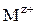 и
и 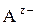 – катион и анион с зарядами z+ и z – соответственно, ν + и ν – – число молей катионов и анионов, образующихся при диссоциации молекул соединения.
– катион и анион с зарядами z+ и z – соответственно, ν + и ν – – число молей катионов и анионов, образующихся при диссоциации молекул соединения.
В соответствии с условием электронейтральности химический потенциал ms соединения  как целого связан с химическими потенциалами составляющими его катионов m+ и анионов m-соотношением
как целого связан с химическими потенциалами составляющими его катионов m+ и анионов m-соотношением
ms = ν +m+ + ν –m–. (2)
Всю совокупность взаимодействий в электролитах формально описывают, используя понятие активности соединений и ионов.
Химический потенциал любой i-й частицы раствора выражается через её активность ai уравнением
mi = 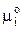 + RT ln ai, (3)
+ RT ln ai, (3)
где 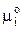 – стандартное значение химического потенциала, соответствующее ai = 1.
– стандартное значение химического потенциала, соответствующее ai = 1.
Используя выражение (3), из уравнения (2), принимая во внимание, что оно справедливо и в стандартных условиях, можно получить связь между активностью растворенного соединения как целого as и активностями катионов a+ и анионов a– в растворе
as = 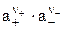 . (4)
. (4)
При описании свойств растворов электролитов обычно вводят понятие средней ионной активности, так как экспериментально определить активность отдельного иона невозможно
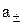 =
= 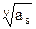 =
= 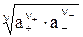 , (5)
, (5)
где ν = ν + + ν –.
Активность частиц выражается в виде произведения концентрации частиц на их коэффициент активности gi
ai = migi, (6)
где mi – моляльная концентрация i-й частицы, хотя концентрацию можно выразить и в других единицах.
Коэффициент активности показывает степень отклонения поведения реального раствора от поведения идеального раствора.
Из выражения (6) следует, что для определения активности иона необходимо знать значения его концентрации и коэффициента активности. Так как определить коэффициент активности отдельного иона также невозможно, то для термодинамической характеристики растворов используют средний коэффициент активности электролита 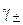 , связанный с коэффициентами активности катионов g+ и анионов g- соотношением, подобным соотношению (5)
, связанный с коэффициентами активности катионов g+ и анионов g- соотношением, подобным соотношению (5)
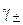 =
= 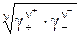 . (7)
. (7)
Аналогично можно ввести понятие средней моляльности
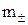 =
= 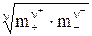 . (8)
. (8)
Так как m+ = ν + m и m– = ν – m, то
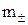 =m
=m  , (9)
, (9)
где m – аналитическая моляльность соединения, m+ – моляльность катиона, m – – моляльность аниона.
Очевидно, что
a+ = m+g+ , a– = m–g– и 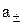 =
= 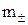
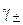 . (10)
. (10)
Средний коэффициент активности электролита и, следовательно, среднюю активность электролита можно определить методом измерения электродвижущих сил гальванических элементов без переноса. Для этого используют элемент, составленный из электродов, один из которых обратим по отношению к катионам, а другой – по отношению к анионам соединения. Электроды опускают в один и тот же раствор электролита.
Для определения активности раствора соляной кислоты применяют гальванический элемент, составленный из хлорсеребряного и водородного электродов, которые обратимы относительно аниона и катиона соляной кислоты соответственно
Сu, Pt, Н2 | НСl | AgCl, Аg, Cu. (11)
Но так как водородный электрод сложен в эксплуатации, то его обычно заменяют хингидронным электродом, с учетом условий применения последнего. Тогда гальваническую цепь можно представить схемой
Сu, Аg, AgCl | НСl, хингидрон | Pt, Cu. (12)
ЭДС Е этого гальванического элемента равна разности между потенциалами хингидронного электрода φ хг и хлорсеребряного электрода φ хл. сер.
Е = φ хг – φ хл. сер. (13)
На поверхности платины в растворе хингидрона устанавливается равновесие
C6H4O2 + 2H+ + 2e 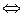 C6H4(OH)2 (14)
C6H4(OH)2 (14)
где C6H4O2 и C6H4(OH)2 – хинон (х) и гидрохинон (гх) соответственно, получающиеся в результате диссоциации хингидрона C6H4O2·C6H4(OH)2 в водном растворе по реакции
C6H4O2·C6H4(OH)2 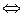 C6H4O2 + C6H4(OH)2. (15)
C6H4O2 + C6H4(OH)2. (15)
Согласно (14) потенциал хингидронного электрода выражается уравнением
φ хг = φ хго + 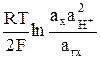 = φ хго +
= φ хго + 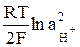 . (16)
. (16)
В последнем выражении учтено, что при избытке хингидрона 
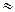 1.
1.
Таким образом, хигидронный электрод обратим по отношению к катионам H+, т.е. к катионам соляной кислоты.
Хлорсеребряный электрод представляет собой электрод второго рода – серебряная проволока, покрытая малорастворимой солью AgCl и опущенная в раствор соляной кислоты. Потенциал электрода выражается уравнением
φ Ag+/Ag = φ оAg+/Ag + 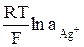 (17)
(17)
Так как в растворе находится малорастворимая соль, и раствор насыщен по отношению к ней, активность ионов металла определяется произведением растворимости AgCl
ПР = 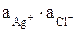 (18)
(18)
Подставив из выражения (18) 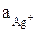 в уравнение (17), получим
в уравнение (17), получим
φ хл.сер = φ Ag+/Agо + 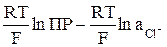 = φ хл.серо
= φ хл.серо 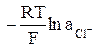 (19)
(19)
Таким образом, хлорсеребряный электрод обратим по отношению к анионам соляной кислоты.
На поверхности серебра хлорсеребряного электрода устанавливается равновесие
AgCl + e 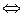 Ag + Cl– (20)
Ag + Cl– (20)
Подставив выражения (16) и (19) для потенциалов электродов в уравнение (13), получим
Е = φ хго – φ хл.серо + 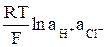 (21)
(21)
Поскольку согласно (5) 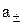 =
= 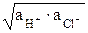 , а разность между стандартными значениями потенциалов равна стандартной ЭДС Ео, то
, а разность между стандартными значениями потенциалов равна стандартной ЭДС Ео, то
Е = Ео + 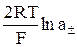 . (22)
. (22)
Подставляя в (22) выражение средней активности электролита через среднюю моляльность и средний коэффициент активности согласно (10) и заменяя среднюю моляльность на аналитическую моляльность согласно (9), получим
Е = Ео + 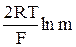 +
+ 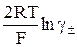 . (23)
. (23)
Откуда
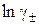 =
=  . (24)
. (24)
Используя определенное экспериментально значение ЭДС (Е) для раствора соляной кислоты заданной концентрации m, по уравнению (24) можно рассчитать средний коэффициент активности 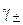 , поскольку стандартные значения потенциалов известны.
, поскольку стандартные значения потенциалов известны.
Зависимость φ хго от температуры определяется уравнением
φ хго = 0, 7177 – 7, 4·10– 4 Т, (25)
где Т – температура, К; φ хго измеряется в Вольтах.
Зависимость φ хл.серо от температуры определяется уравнением
φ хл.серо = 0, 222 – 6, 4·10-4(t –25) – 3, 2·10-6(t – 25), (26)
где t – температура, оС; φ хл.серо измеряется в Вольтах.
По значению 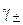 для раствора заданной концентрации легко определить
для раствора заданной концентрации легко определить 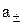 ,
,  и
и 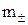 .
.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Цель работы – установление зависимости средней активности и среднего коэффициента активности электролита от его концентрации.
Порядок выполнения работы
1. Готовят 5 – 6 растворов соляной кислоты с моляльностями в интервале от 0, 001 до 0, 1. Конкретные значения объемов и концентраций растворов задает преподаватель.
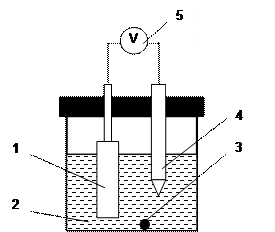
2. Собирают установку для измерения ЭДС исследуемой гальванической цепи Сu, Аg, AgCl | НСl, хингидрон | Pt, Cu (см. рис.1).
 |
3. Измеряют ЭДС гальванической цепи для растворов всех заданных концентраций соляной кислоты компенсационным методом.
Рис1. Схема установки для измерения ЭДС гальванического элемента. 1 – платиновый электрод; 2 – электролит; 3– хингидрон; 4 – электрод сравнения; 5 – высокоомный потенциометр
Обработка результатов опыта
1. Рассчитывают средний коэффициент активности соляной кислоты для заданных её концентраций, используя уравнение (24).
2. По уравнениям (9), (10) и (5), и рассчитывают значения 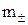 ,
, 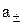 и
и  для заданных концентраций соляной кислоты.
для заданных концентраций соляной кислоты.
3. Рассчитывают ионную силу растворов соляной кислоты заданных концентраций по уравнению
I = 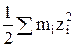 , (27)
, (27)
где mi и zi – моляльная концентрация и заряд i-го иона в растворе.
4. Строят график в координатах lg 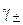 –
– 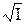 и сравнивают его с подобной зависимостью, полученной в теории Дебая-Хюкеля для сильных электролитов.
и сравнивают его с подобной зависимостью, полученной в теории Дебая-Хюкеля для сильных электролитов.
5. Измеренные и рассчитанные величины сводят в таблицу 1. Перед таблицей привести значение стандартной ЭДС.
Таблица 1. Измеренные и рассчитанные величины.
| Концентрация, моль/1000 г | Е, В | aHCl | 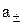
| 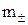
| 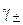
| lg 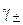
| I | 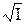
|
По результатам работы делают выводы и вычисляют абсолютную и относительную ошибки.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Вывести уравнение связи между средней активностью электролита и моляльной концентрацией.
2. Электродные реакции на хингидронном электроде и уравнение Нернста для электродного потенциала.
3. Электродные реакции на хлорсеребряном электроде и уравнение Нернста для электродного потенциала.
4. Вывести уравнение связи средней активностью электролита и коэффициента активности электролита с ЭДС между хингидронным и хлорсеребряным электродом.
5. Нарисовать электрическую схему установки для измерения ЭДС.
6. Написать схему электрохимической цепи используемой в работе.
7. Зависимость коэффициента активности от температуры.
8. Что представляет собой окислительно-восстановительный электрод?
9. Как выразить константу равновесия реакции, используя стандартные окислительно-восстановительные потенциалы?
10.Зная зависимость потенциала электрода от температуры найти число электронов, участвующих в электродной реакции.
11. Рассчитайте изменения термодинамических функций для реакции
Cd + Hg2SO4 = CdSO4 + 2Hg, если зависимость от температуры ЭДС гальванического элемента, в котором протекает реакция, описывается уравнением:
Е = 1, 083 – 4, 06·10-5(t –20), где t – температура, оС.
12. Размерности величин в уравнениях.